X,Y,Z have same molecular formula (C3H4) but X,Y,Z have different IUPAC name. If X is cyclic alkene and Y is alkyne then what is true about Z.
Z is cyclic alkene
Z is alkyne
Z is CH2=C=CH2
All of these
The correct Answer is:C
Z can not be cyclic and alkyne
So Z is CH2=C=CH2 O(g)→O2−(g),as no. of electronZeff↓∴size↑↑⏐
⏐
⏐⏐
Topper's Solved these Questions
Similar Questions
The gaseous reaction
2A(g)+nB(g)⇔mC(g) is represented by following curves.

What is the value of m+n?
View SolutionThe gaseous reaction
2A(g)+nB(g)⇔mC(g) is represented by following curves.

What is the value of m+n?
View Solution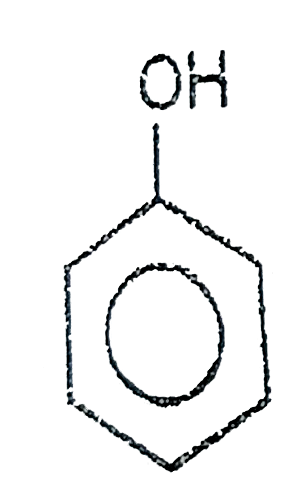 , CO2/NaOH−−−−−−−−−→H+(A)Acetic Anhydride−−−−−−−−−→Aspirin(B)
, CO2/NaOH−−−−−−−−−→H+(A)Acetic Anhydride−−−−−−−−−→Aspirin(B)
Product B is
View SolutionProve the identities: ∣∣ ∣ ∣∣zxyz2x2y2z4x4y4∣∣ ∣ ∣∣=∣∣ ∣ ∣∣xyzx2y2z2x4y4z4∣∣ ∣ ∣∣=∣∣ ∣ ∣∣x2y2z2x4y4z4xyz∣∣ ∣ ∣∣ =x y z (x-y)(y-z)(z-x)(x+y+z)
View Solution(x+y)3+(y+z)3+(z+x)3−3(x+y)(y+z)(z+x)
View Solution(x+y)3+(y+z)3+(z+x)3−3(x+y)(y+z)(z+x)
View SolutionIf x, y, z are three sums of money such that y is the simple interest on x, z is the simple interest on y for the same time and at the same rate of interest, then we have x2=yz (b) y2=xz (c) z2=xy (d) xyz=1
View SolutionTwo hydrocarbons (X) and (Y) have the same molecular formula C3H6 Baeyer's reagent canb e colourised by (X) but not by (Y). Both (X) and (Y) on catalytic hydrogenation gives same product (Z). Identity X,Y and Z.
View Solutionसिद्ध कीजिए।
∣∣ ∣ ∣∣111xyzx3y3z3∣∣ ∣ ∣∣=(x−y)(y−z)(z−x)(x+y+z)
View Solutionसिद्ध कीजिए कि
∣∣ ∣∣.xC1.xC2.xC3.yC1.yC2.yC3.zC1.zC2.zC3∣∣ ∣∣=xyz(x−y)(y−z)(z−x)12.
View Solution(x−y)3+(y−z)3+(z−x)3(x−y)(y−z)(z−x)=
View SolutionShow that ∣∣ ∣ ∣∣x+yy+zz+xy+zz+xx+yz+xx+yy+z∣∣ ∣ ∣∣=2[3xyz−x3−y3−z3]
View Solutionপ্রমাণ করো
∣∣ ∣ ∣∣y+zz+xx+yz+xx+yy+zx+yy+zz+x∣∣ ∣ ∣∣=2∣∣ ∣ ∣∣xyzyzxzxy∣∣ ∣ ∣∣=−2(x3+y3+z3−3xyz)
View SolutionA(x,y,z)= min. (x+y,y+z,z+x)
B(x,y,z)=max (x−y,y−z,z−x)
C(x,y,z)= max(A(x,y,z),B(x,y,z))
D(x,y,z)= min (A(x,y,z),B(x,y,z))
What is the value of A(2,3,4)+B(2,3,4)?
View SolutionProve the identities: ∣∣ ∣ ∣∣zxyz2x2y2z4x4y4∣∣ ∣ ∣∣=∣∣ ∣ ∣∣xyzx2y2z2x4y4z4∣∣ ∣ ∣∣=∣∣ ∣ ∣∣x2y2z2x4y4z4xyz∣∣ ∣ ∣∣ =x y z (x-y)(y-z)(z-x)(x+y+z)
View Solution
