Assume that all the pulleys are massless and frictionless and strings to be inextensible.
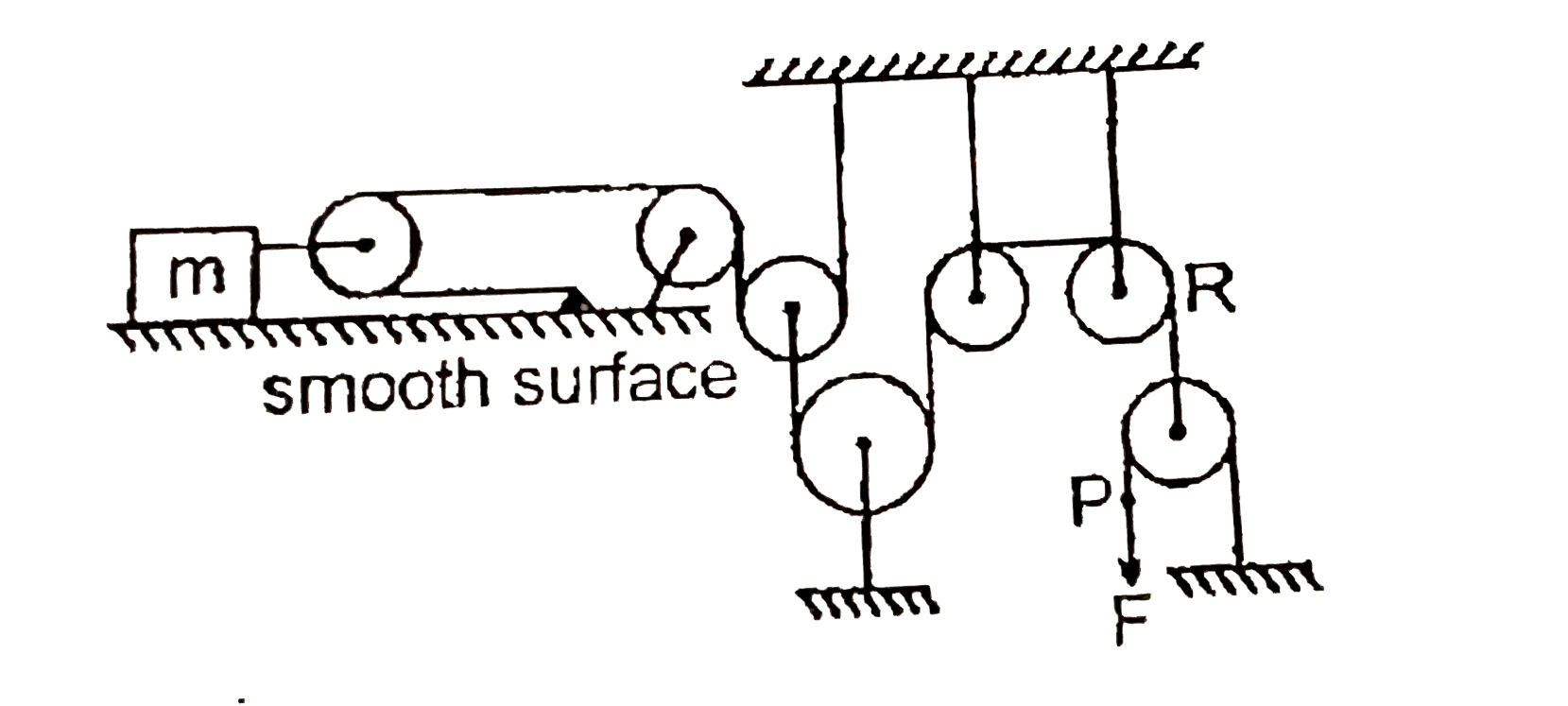
Acceleration of P is 4 F/m
Acceleration of m is F/m
Acceleration of P is 2F/m
Acceleration of m is F/2m
The correct Answer is:B
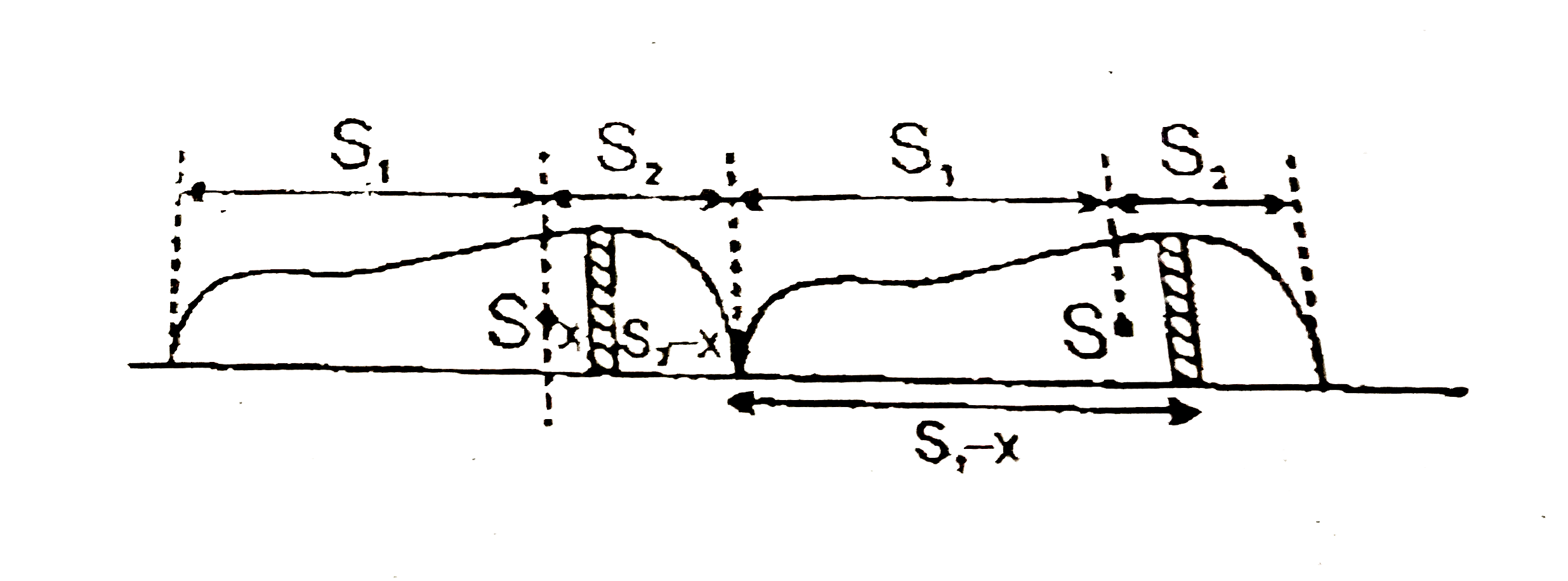
W1=∫[μ1dmg(S2−x)+μ2dmg(S1+x)]
=μ1S2g∫dm+μ2S1g∫dm+(μ2−μ1)g∫dmx
=(μ1S2+μ2S1)Mg
as ∫xdm=0=MtotalXcm=0
Similar Questions
Find the acceleration of masses m_(1) and m_(2) connected by an inextensible string, shown in figure-2.13(a). The string and pulley are assumed to be massless and frictionless.
View SolutionFind the accelerations of two blocks. Assume pulleys and strings are massless and frictionless. Also assume the string to be inextensible.
View SolutionFind the relation between acceleration of the two blocks m_(1) and m_(2) . Assume pulleys are massless and frictionless and the strings are inextensible .
View SolutionIn the system shown in the given figure, the inline is frictionless, the string is massless, and inextensible pulley is light and frictionless. The system is released from rest.

View SolutionFind the acceleration of two masses as shown in figure . The pulley are light and frictionless and string are light and frictionless and string are light and inextensible.
View SolutionFigure shows an arrangement of pulleys and two blocks. All surfaces are frictionless . All pulleys and strings are massless. All string are smooth and massless. The acceleration of block A is :
View SolutionFigure shows an arrangement of pulleys and two blocks. All surfaces are frictionless . All pulleys and strings are massless. All string are smooth and massless.

Normal reaction between A and ground is :
View Solution

