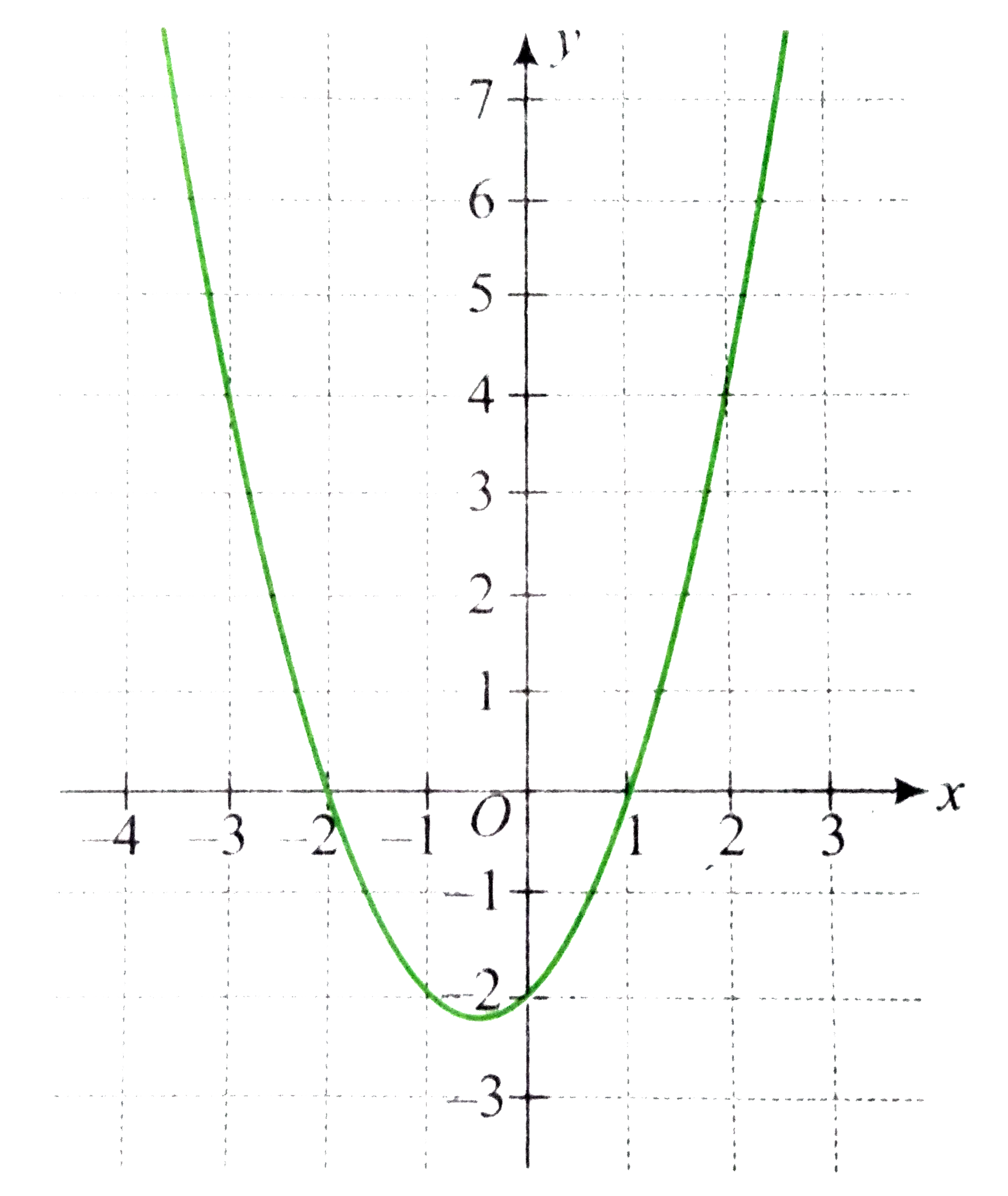
Consider the graph of y = f(x) as shown in the following figure.
(i) Find the sum of the roots of the equation f (x) = 0.
(ii) Find the product of the roots of the equation f(x) = 4.
(iii) Find the absolute value of the difference of the roots of the equation f(x) = x+2 .
Text Solution

(i) Roots of the equation f(x) = 0 occur where the graph of y = f(x) and y = 0 intersect.
From the diagram, the points of intersection of intersection are x =- 2 and x= 1. Hence sum of the roots is - 1.
(ii) Roots of the equation f(x) = 4 occur where the graph of y = f(x) and y = 4 intersect. From the diagram, the points of intersection are x =- 3 and x = 2. Hence the product of the roots is -6.
(iii) Roots of the equation f(x) = x+2 occur where the graph of y = f(x) and y = x+2 intersect. From the diagram, the points of intersection are x =- 2 and x = 2. Hence the difference of the roots is 4.
|
Topper's Solved these Questions
- GETTING STARTED WITH GRAPHSBOOK - CENGAGECHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercise
18 Videos
- FUNCTIONSBOOK - CENGAGECHAPTER - FUNCTIONSEXERCISE - Question Bank
30 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
18 Videos
Similar Questions
Knowledge Check
The two roots of the equation f(x)=f(x+8x−1) are:
A2,-2B4,-2C−4,−2D2,4The two roots of the equation f(x)=f(x+8x−1) are :
A2,−2B4,−2C−4,−2D2,4
Find the number of real roots of the equation f(x)=x3+2x2+x+2=0
View SolutionIf the sum of the roots of the equation (a+1)x2+(2a+3)x+(3a+4)=0 is −1, then find the product of the roots.
View SolutionThe equation whose roots are reciprocals of the roots of the equation f(x)=0 is
View SolutionIf one root of the quadratic equation x2+6x+2=0 is, 23 then find the other root of the equation.
View SolutionFind the absolute value of the difference of the real roots of the equation x2−22010x+∣∣x−22009∣∣+2(24017−1)=0
View Solutionif the sum of roots of the quadratic equation,x2−(p+4)x+5=0 is 0 find the value of p
View Solution