Let f(x) ={−X2+(b3−b2+b−1)(b2+3b+2)}2X−3 1<X<30≤X<1
Find al possible values of b such that f(x) has the smallest values at x=1
Such problems can easily be solved by graphical approach (as in figure).
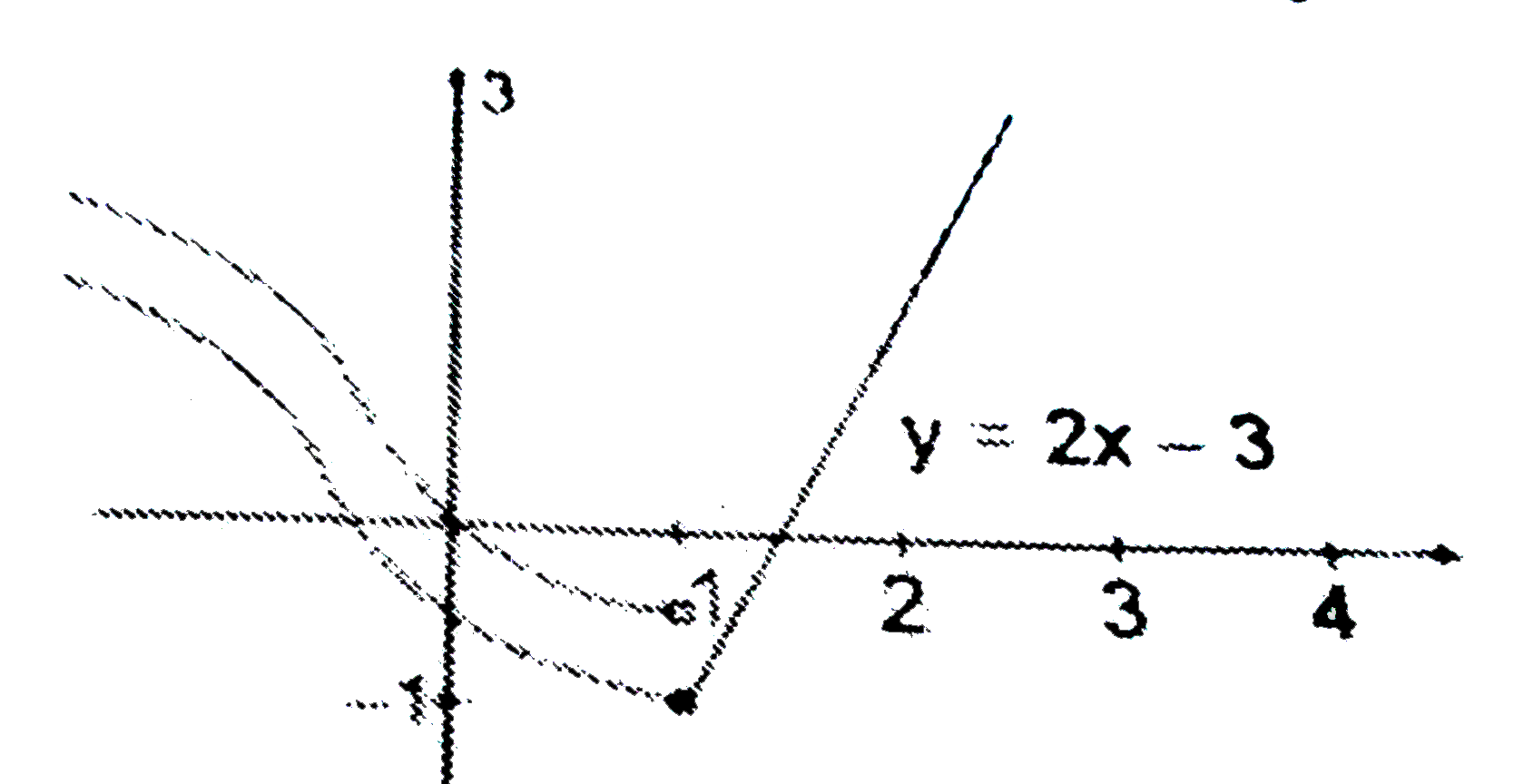
Hence the limiting value of f(x) from of x=1 should b either greater of equal to the value of function at x=1.
limx→1f(x)≤f(1)
⇒ −1+(b3−b2+b−1)(b2+3b+2)≤−1
⇒ (b2+1)(b−1)(b+1)(b+2)≥0
⇒ b∈(−2,−1)∪[1,+∞)
Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBook:RESONANCEChapter:APPLICATION OF DERIVATIVESExercise:Self Practice Problems
Explore 34 Videos
- APPLICATION OF DERIVATIVESBook:RESONANCEChapter:APPLICATION OF DERIVATIVESExercise:Exersise -1A
Explore 5 Videos
- COMBINATORICSBook:RESONANCEChapter:COMBINATORICSExercise:Exercise-2 (Part-II: Previously Asked Question of RMO)
Explore 8 Videos
Similar Questions
Find the slope of the normal to the curve x=1−asinθ,y=bcos2θat θ=π2.
View Solution(i) Find the equation of tangent to curve y=3x2+4x+5 at (0,5)
(ii) Find the equation of tangent and normal to the curve x2+3xy+y2=5 at point (1,1) on it
(iii) Find the equation of tangent and normal to the curvex=2at21+t2,y=2at21+t2 at the point for which t=12
(iv) Find the equation of tangent to the curve ={x2sin1/x0 x=0 x≠0x=0 at (0,0)
View SolutionFind the number of all 6-digit natural numbers such that the sum of their digits is 10 and each of the digits 0,1,2,3 occurs at least once in them.
View Solutionlet f(x)=-x^(3)+(b^(3)-b^(2)+b-1)/(b^(2)+3b+2) if x is 0 to 1 and f(x)=2x-3 if x if 1 to 3. All possible real values of b such that f(x) has the smallest value at x=1 are
View SolutionFind the value of a + b if f(x) = {((a e^(1//|x+2|) - 1)/(2-e^(1//|x+2|)),; -3 lt x lt -2), (b,; x = -2), (sin((x^4-16)/(x^5+32)),; -2 lt x lt 0):} is continuous at x = -2.
View SolutionLet f(x) ={3−x 0≤x<1x2+xb x≥1. Find the set of values of b such that f(x) has a local minima at x=1.
View SolutionLet f(x)={3x2−2x+10x<1−2x>1
The set of values of b for which f(x) has greatest value at x=1 is
View SolutionIf f(x)=⎧⎪⎨⎪⎩x−1, for 1≤x<22, for x=22x−3, for 2<x<3, then f has removable discontinuity at x=2, if f(2)=
View SolutionIf f(x)=⎧⎪⎨⎪⎩ax2−b, for 0≤x<12, for x=1x+1, for 1<x≤2 is continuous at x=1 , then the most suitable values of a, b are
View SolutionIf Ltx→0(1+ax+bx2)2x=e2, then the value of a and b are
View Solutionमाना f(x)=⎧⎪⎨⎪⎩−x3+(b3−b2+b−1)(b2+3b+2)0≤x≤12x−31≤x≤3b के सभी संभव वास्तविक मान ज्ञात कीजिए जिनके लिए x=1 पर f(x) क मान निम्नतम हो।
View SolutionIf the function f(x)=⎧⎪⎨⎪⎩Ax−Bx≤13x1<x<2Bx2−Ax≥2
is continuous at x=1 and discontinuous at x=2,
find the values of AandB.
View Solutionlet f(x)=−x3+b3−b2+b−1b2+3b+2 if x is 0 to 1 and f(x)=2x−3 if x if 1 to 3.All possible real values of b such that f(x) has the smallest value at x=1 are
View SolutionFind the value of a,b if f(x)=⎧⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪⎩ae1/|x+2|−12−e1/|x+2|;−3<x<−2b;x=−2sin(x4−16x5+32);−2<x<0 is continuous at x=−2.
View Solutionमाना f(x)=⎧⎪⎨⎪⎩−x3+(b3−b2+b−1)(b2+3b+2),0≤x<12x−3,1≤x≤3 है। b के सभी संभव वास्तविक मान ज्ञात कीजिए ताकि f(x) का न्यूनतम मान x=1 पर हो।
View Solution
