Consider a force acting on a particle given as →F=yˆi+xˆj , where ( x, y ) is the instantaneous location of the particle. This type of force is :
Surely a conservation force
Surely a non-conservation force
Information insufficient to reach to a conclusion
Will be conservation only if the particle is constrained to move in the x-y plane.
The correct Answer is:A
Similar Questions
Knowledge Check
Force acting on a particle is given by F=A−xBt, where x is in metre and t is in seconds. The dimensions of B is -
AMLT−2BM−1T−3CM−1TDMT−1Path traced by a moving particle in space is called trajectory of the particle. Shape of trajectiry is decided by the forces acting on the particle. When a coordinate system is associated with a particle motion, the curve equation in which the particle moves [y=f(x)] is called equation of trajectory. It is just giving us the relation among x and y coordinates of the particle i.e. the locus of particle. To find equation of trajectory of a particle, find first x and y coordinates of the particle as a function of time eliminate the time factor.
The position vector of car w.r.t. its starting point is given as →r=atˆi−bt2ˆj where a and b are positive constants. The locus of a particle is:-Aa2y+bx2=0Ba2y=bx2Cy=ba2Day2=b2xA particle has initial velocity →v=3ˆi+4ˆj and a constant force →F=4ˆi−3ˆj acts on the particle. The path of the particle is :
Astraight lineBparabolicCcircularDelliptical
A particle of mass 'm' moves along the quarter section of the circular path whose centre is at the origin . The radius of the circular path is 'a'. A force →F=yˆi−xˆj newton acts on the particle, where x,y denote the coordinates of position of the particle. Calculate the work done by this force in taking, the particle from point, A(a,0) to point B(0,a) along the circular path.
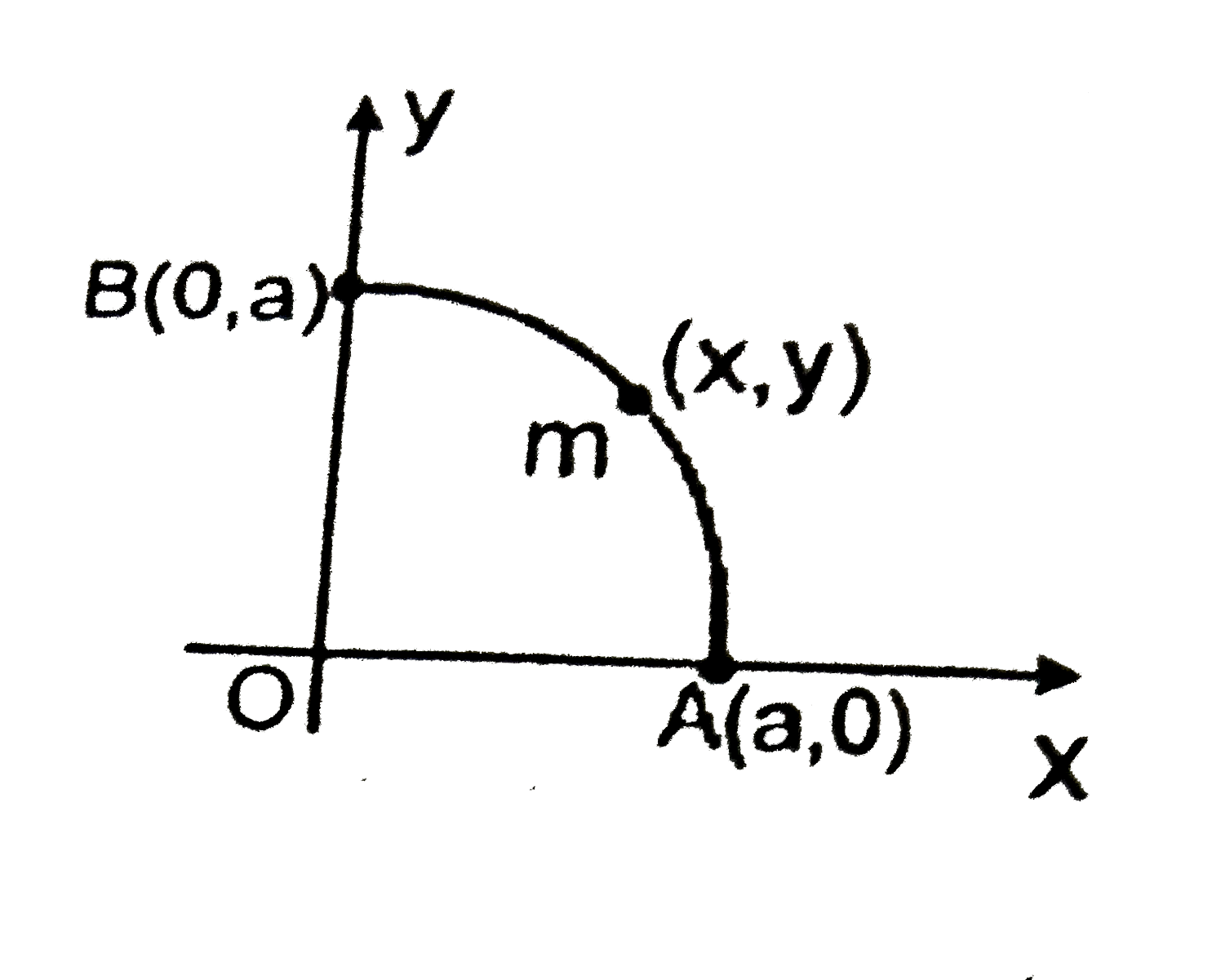
View SolutionThe position vector of a particle is given by →r=kcosωˆi+ksinωˆj=xˆi+yˆj, where k and ω are constants and t time. Find the angle between the position vector and the velocity vector. Also determine the trajectory of the particle.
View SolutionA particle with charge +Q is moving on X−Y plane.
Magnetic field existing in the region is given as →B=Boˆk.
At a certain instant of time net magnetic force acting on the particle is →F=F0ˆi+2F0ˆj. Find the instantaneous velocity of particle.
View SolutionA particle of mass 2kg moves under a force given by
→F=−(8N/m)(xˆi+yˆj)
where ˆi and ˆj are unit vectors in the x and y directions.
The particle is projected from the origin in xy plane with an initial velocity →v=(3m/s)ˆi+(4m/s)ˆj.
Select correct statement(s).
View SolutionWhen force →F1,→F2,→F3 are acting on a particle of mass m, the particle remains in equilibrium. If the force →F1 is now removed then the acceleration of the particle is :
View Solution

