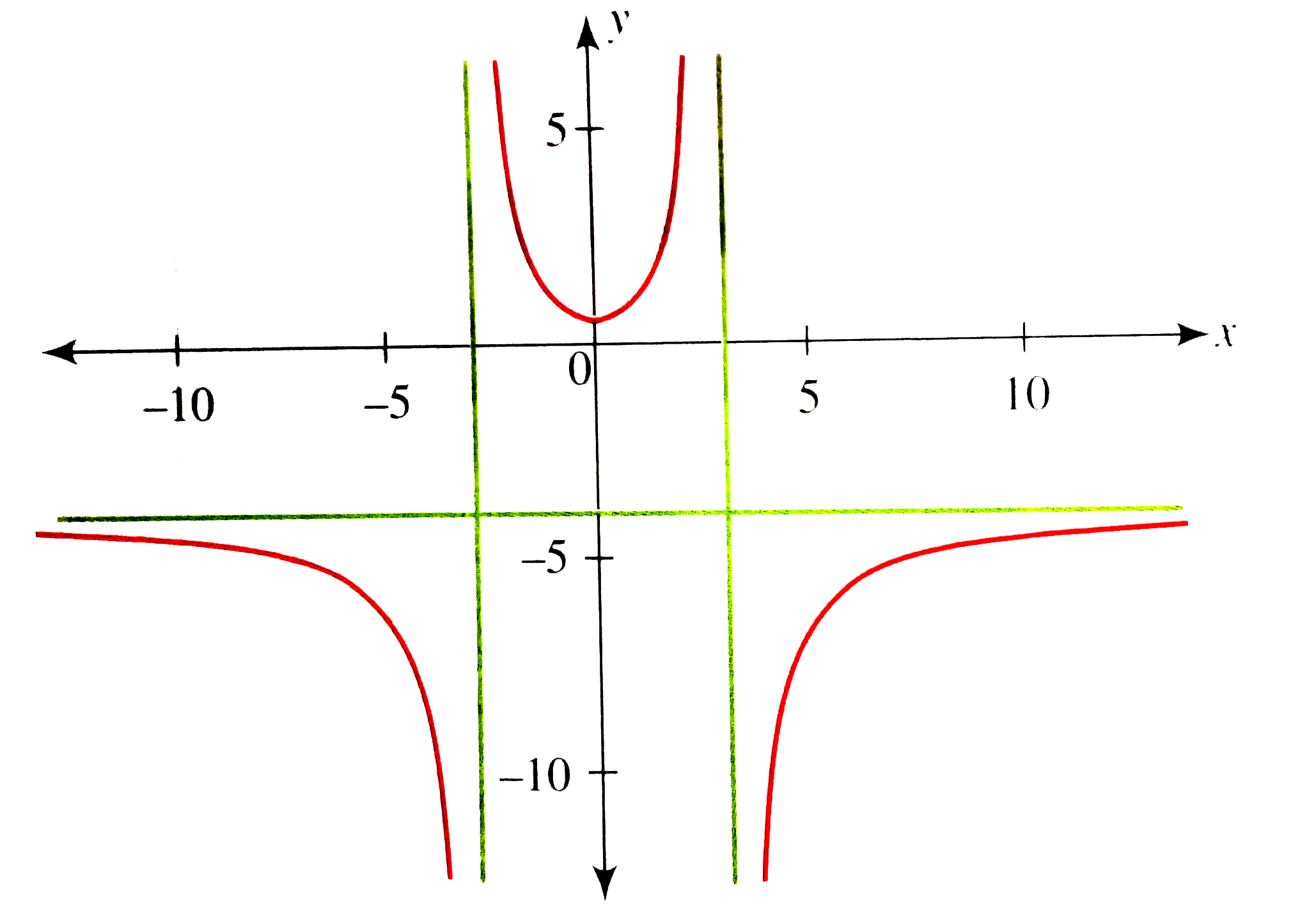
Write a rational function g with vertical asymptotes at x = 3 and x = -3, a horizontal asymptote at y = -4 and with no x-intercept.
⋅ Since g has vertical is asymptotes x = 3 and x = -3, then the denominator of the rational function contains the product of (x-3) and (x+3) . Function g has the form
g(x)=h(x)(x−3)(x+3)
⋅ For the horizontal asymptote to exist, the numerator h(x) of g(x) has same degree as that of the denominator with a leading coefficient equal to -4. At the same time, h(x) has no real zeros. Hence
f(x)=−4x2−6(x−3)(x+3)
⋅ Check the characteristics in the graph of g shown below.
Topper's Solved these Questions
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBook:CENGAGEChapter:GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSExercise:Exercise
Explore 13 Videos
- GRAPHICAL TRANSFORMATIONSBook:CENGAGEChapter:GRAPHICAL TRANSFORMATIONSExercise:Exercise
Explore 22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS Book:CENGAGEChapter:GRAPHS OF ELEMENTARY FUNCTIONS Exercise:Exercise
Explore 34 Videos
Similar Questions
Write a possible rational function h with a hole at x = 5, a vertical asymptote at x = -1, a horizontal asymptote at y = 2 and x-intercept at x = 2.
View SolutionWrite a possible rational function f that has a vertical asymptote at x = 2, a horizontal asymptote y = 3 and a zero at x = -5. Also draw the graph of the function.
View SolutionWrite a possible rational function f that has a vertical asymptote at x = 2, a horizontal asymptote y = 3 and a zero at x = -5. Also draw the graph of the function.
View SolutionWrite a rational function f with a slant asymptote y=x+4, a vertical asymptote at x = 5 and one of the zeros at x = 2.
View SolutionWrite a rational function f with a slant asymptote y=x+4, a vertical asymptote at x = 5 and one of the zeros at x = 2.
View SolutionFind the asymptotes of the curve xy−3y−2x=0 .
View SolutionFind all the vertical asymptotes and holes of (x+3)(x−7)(2x−5).
View Solution(a) Can the graph of the function intersect the horizontal asymptote?
(b) Can the graph of the function intersect the vertical asymptote?
View Solution(a) Can the graph of the function intersect the horizontal asymptote?
(b) Can the graph of the function intersect the vertical asymptote?
View SolutionFind the eccentricity of the hyperbola with asymptotes 3x+4y=2 and 4x−3y=1
View Solution

