Plot the region satisfying |x|+|y|≤2and|x|+|y|>2.
|x|+|y|≤2
∴ ⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩x+y≤2,x≥0,y≥0x−y≤2,x≥0,y≤0−x+y≤2,x≤0,y≥0−x−y≤2,x≤0,y≤0
For x≥0,y≥0andx+y≤2, we have the following region.
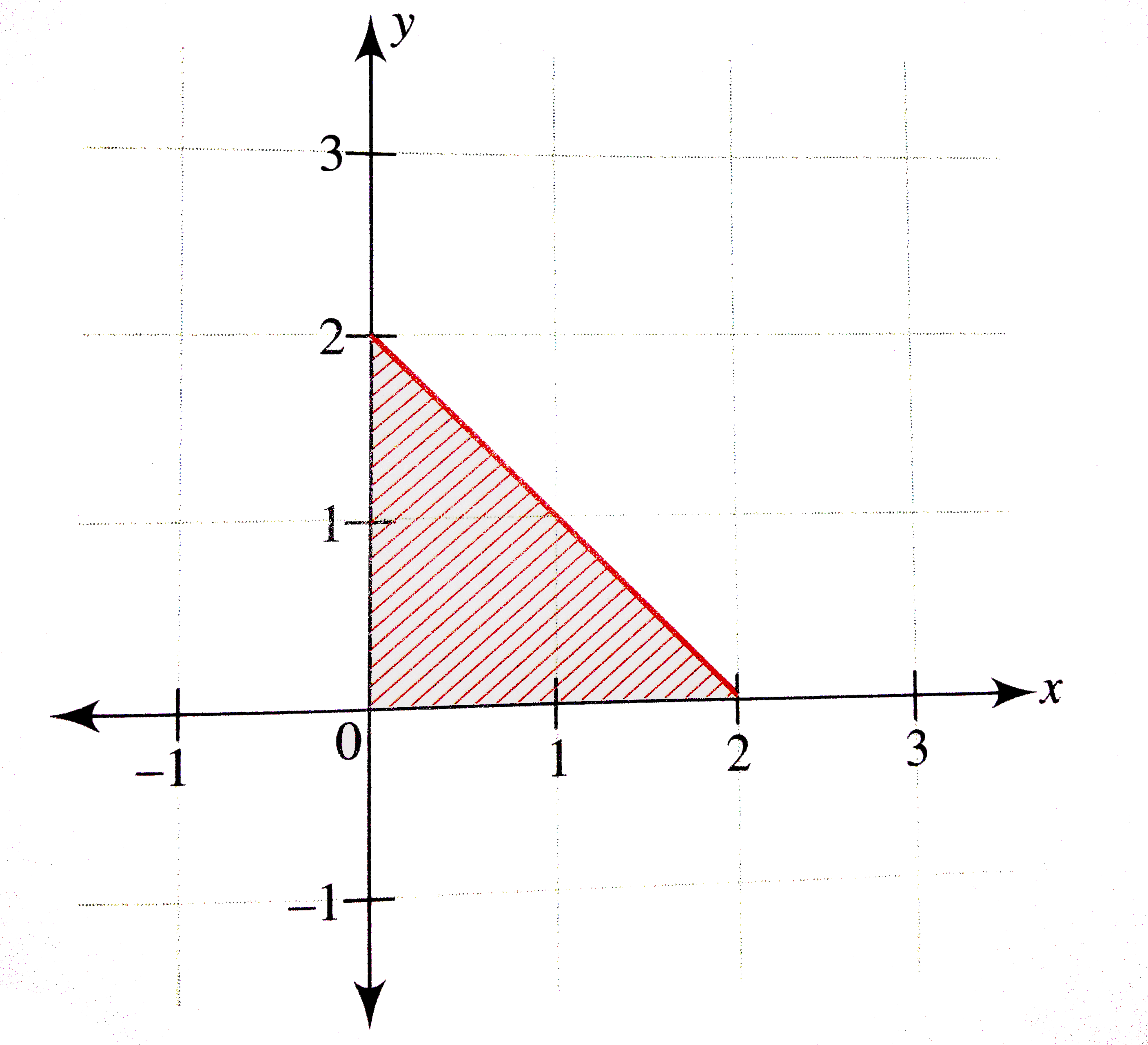
Similarly, we have other three triangles, one in each quadrant.
Clubbing all four cases, we have the following region as a square.

Clearly, the points satisfying |x|+|y|>2 lie outside the square.
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS Book:CENGAGEChapter:GRAPHS OF ELEMENTARY FUNCTIONS Exercise:Exercise
Explore 34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBook:CENGAGEChapter:GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSExercise:Exercise
Explore 13 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBook:CENGAGEChapter:GRAPHS OF TRIGONOMETRIC FUNCTIONSExercise:Exercise
Explore 22 Videos
Similar Questions
Plot the region 6x+2y≥31
View SolutionFind the area of the region formed by the points satisfying
|x|+|y|+|x+y|≤2.
View SolutionFind the area of the region formed by the points satisfying
|x|+|y|+|x+y|≤2.
View SolutionPlot the region of the points P (x,y) satisfying |x|+|y|<1.
View SolutionPlot the region of the points P (x,y) satisfying |x|+|y|<1.
View SolutionSketch the region of the points satisfying max.{|x|,|y|}≤4.
View SolutionSketch the region of the points satisfying max.{|x|,|y|}≤4.
View SolutionFind tha area of the region containing the points (x,y) satisfying 4≤x2+y2≤2(|x|+|y|).
View SolutionFind tha area of the region containing the points (x,y) satisfying 4≤x2+y2≤2(|x|+|y|).
View SolutionFind the area of the region which is inside the parabola satisfying the condition |x−2y|+|x+2y|≤8 and xy≥2.
View Solution

