Consider the inequality, 9x−a.3x−a+3≤0, where 'a' is a real parameter.
(a) Find the value of 'a' for which the inequality has at least one negative solution.
(b) Find the values of 'a' for which the inequality has at least one positive solution.
(c) Find the vlaues of 'a' for which the inequality has at least one real solution.
Text Solution
9x−a.3x−a+3≤0
Let t=3x
⇒ t2−at−a+3≤0
or t2+3≤a(t+1) (i)
where t∈R+ for ∀x∈R

Let f1(t)=t2+3andf2(t)=a(t+1)
(a) For x<0,t∈(0,1). That means (i) should have at least one solution in t∈(0,1).
From (i), it is obvious that a∈R+.
Now f2(t)=a(t+1) represents a straight line. It should meet the curve.
f1(t)=t2+3, at least once in t∈(0,1).
f1(0)=3,f1(0)⇒a=3,iff1(1)=f2(1)=a=2
Hence required a∈(2,3).
(b) For at least one positive solution, t∈(1,∞). That means the graphs of f1(t)=t2+3andf2(t)=a(t+1) should meet at least once in t∈(1,∞).
If a=2, both curves touch each other at (1,4).
Hence required a∈(2,∞).
(c) In this case, both graphs should meet at least once in t∈(0,∞).
For a=2, both curves touch, hence required a∈[2,∞).
|
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise
13 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
Similar Questions
Knowledge Check
Which inequality has the following number line solution:
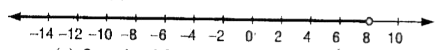 A2x−4<16B2x−6<10C2x−6>12D2x−4>16
A2x−4<16B2x−6<10C2x−6>12D2x−4>16Consider the inequation 9x−a3x−a+3≤0, where a is real parameter.
The given inequality has at least one real solutions for a∈.A(−∞,3)B[2,∞)C(3,∞)D[−2,∞)Consider the inequation 9x−a3x−a+3≤0, where a is real parameter.
The given inequality has at least one negative soluiton for a∈A(−∞,2)B(3,∞)C(−2,∞)D(2,3)
Find the possible values of 'a' such that the inequality 3−x2>|x−a| has atleast one negative solution
View SolutionFind the value of a for which ax2+(a−3)x+1<0 for at least one positive real x.
View SolutionThe set of values of 'a' for which the inequality x2−(a+2)x−(a+3)<0is satisfied by atleast one positive real x,
View SolutionFind the number of integral values of k for which the equation 7cosx+5sinx=2k+1 has at least one solution.
View SolutionSum of integral values of n such that sinx(2sinx+cosx)=n, has at least one real solution is
View Solution

