Draw the graph of the function f(x)=∣∣∣(x+12)[x]∣∣∣,−2≤x≤2, where [⋅] denotes the greatest integer function. Find the points of discontinuity and non-differentiability.
Text Solution
Here, f(x)=∣∣∣(x+12)[x]∣∣∣,−2≤x≤2
⇒ f(x)=⎧⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪⎩∣∣(x+12)(−2)∣∣,−2≤x<−1∣∣(x+12)(−1)∣∣,−1≤x<0∣∣(x+12)(0)∣∣,0≤x<1∣∣(x+12)(1)∣∣,1≤x<2∣∣32⋅2∣∣,x=2
⇒ =⎧⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪⎩−(2x+1),−2≤x<−1−(x+1/2),−1≤x<−1/2(x+1/2),−12≤x<00,0≤x<1x+12,1≤x<23,x=2
The graph of the function is as shown in the following figure.
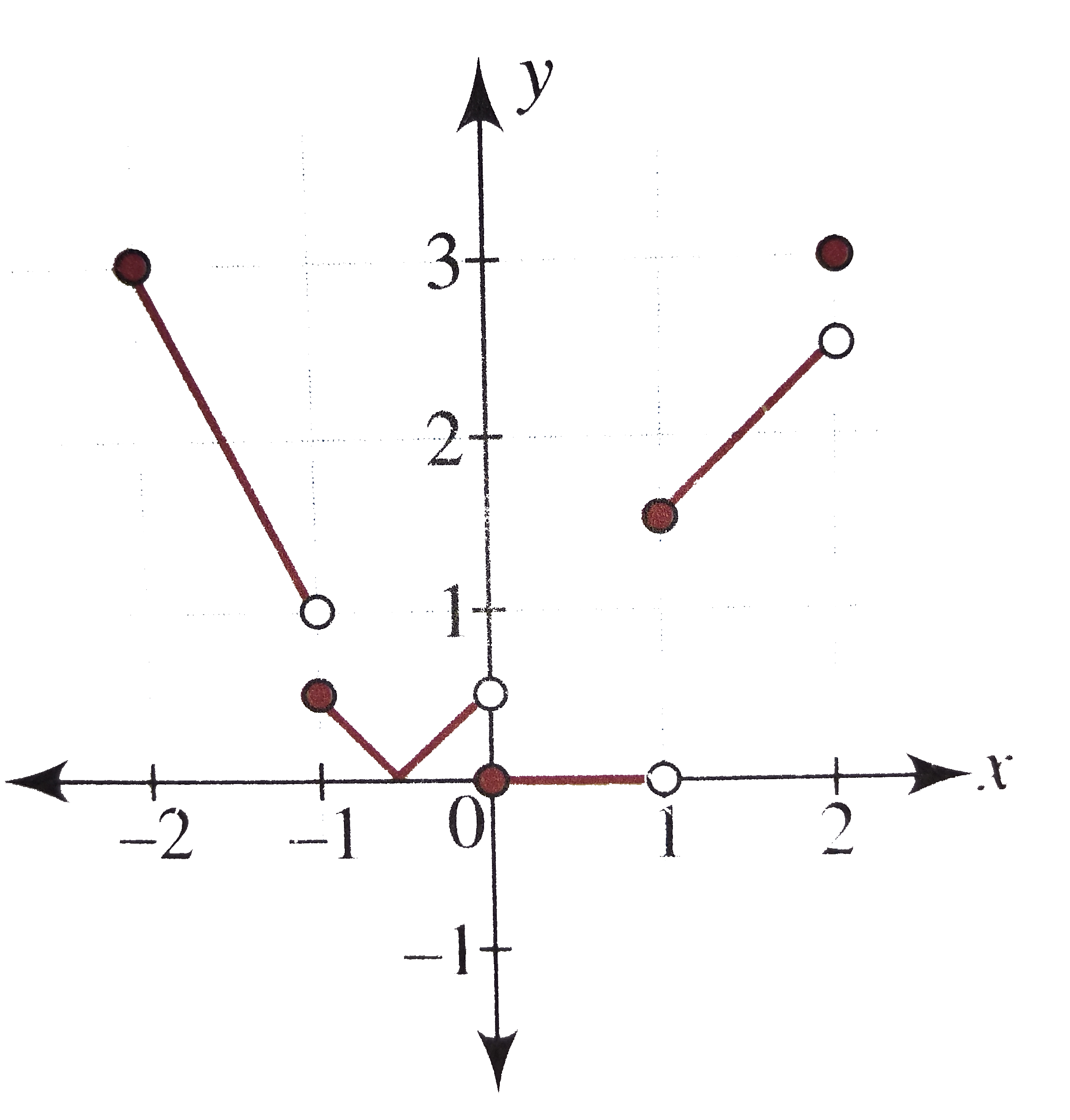
From the figure, f(x) is not continuous as x={−1,0,1,2} as at these points, the graph is broken and f(x) is not differentiable.
At x={−1,−12,0,1,2} as at {−1,0,1,2}, the graph is broken and x=−1/2, there is a sharp edge.
|
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise
13 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
Similar Questions
Knowledge Check
The domain of function f(x)=log[x+12](2x2+x−1), where [.] denotes the greatest integer function is :
A[32,∞)B(2,∞)C(−12,∞)−{12}D(12,1)∪(1,∞)Let f(x)=x2+1[x],1<x≤3.9.[.] denotes the greatest integer function. Then
Af (x) is increasing functionBf (x) is decreasing functionCThe greatest value of f (x) is 13×16.21DThe least value of f (x) is 2Let f(x)=x2+2[x],1≤x≤3, where [.] is the greatest integer function. Then the least value of f(x) is
A2B3C3/2D1
Draw the graph of f(x)=[x2],x∈[0,2), where [⋅] denotes the greatest integer function.
View SolutionThe domain of the function f(x)=1√[x]2−2[x]−8 is, where [*] denotes greatest integer function
View SolutionDraw the graph of f(x)=[tanx],0≤x≤5π/12, where [⋅] represents the greatest integer function.
View SolutionDraw the graph of y=[|x|], where [.] denotes the greatest integer function.
View SolutionIf f(x)={x[x]0≤x<2(x−1)[x]2≤x<3 where [.] denotes the greatest integer function, then
View Solution

