Given f(x) is a periodic function with period 2 and it is defined as
f(x)=⎧⎨⎩[cosπx2]+1,0<x<12−x,1≤x<2
Here [⋅] represents the greatest integer ≤x. If f(0)=1, then draw the graph of the function for x∈[−2,2].
Text Solution
f(x)=⎧⎨⎩[cosπx2]+1,0<x<12−x,1≤x<2
={1,0<x<12−x,1≤x<2

Since the function if periodic with period '2', the required graph for x∈[−2,1] is as follows.
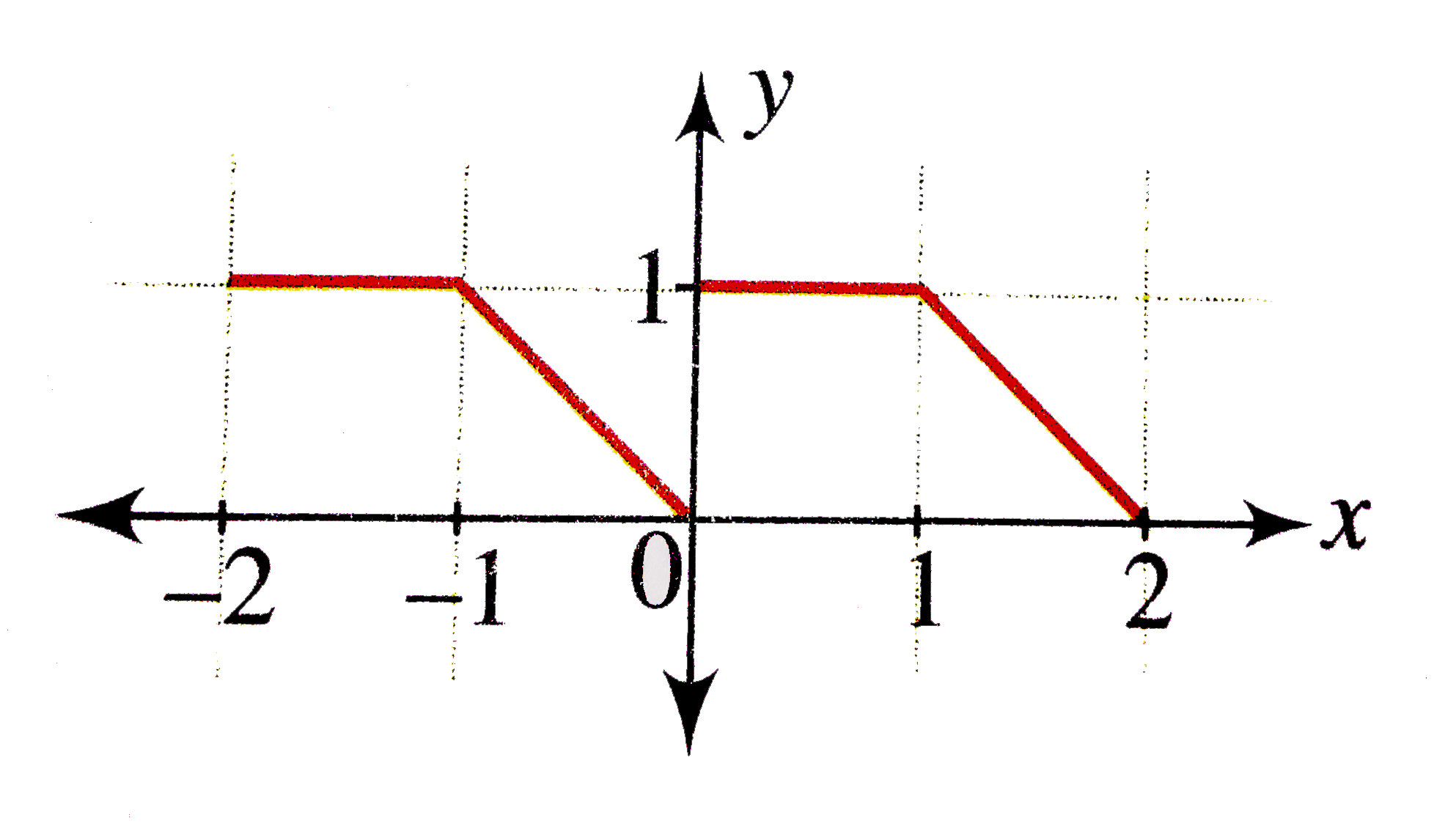
|
Similar Questions
Knowledge Check
If f(x)={∣∣1−4x2∣∣,0≤x<1[x2−2x],1≤x<2, where [] denotes the greatest integer function, then
Af(x) is continuous for all x∈[0,2)Bf(x) is differentiable for all x∈[0,2)−{1}Cf(X) is differentiable for all x∈[0,2)−{12,1}DNone of theseIf f(x)={x2+10≤x<1−3x+51≤x≤2
AIt has a relative minimum at x = 1BIt has a relative maximum at x =1CIt is not continuous at x = 1DNone of theseIf f(x)={x[x]0≤x<2(x−1)[x]2≤x<3 where [.] denotes the greatest integer function, then
Aboth f'(1) and f'(2) do not existBf'(1) exist but f'(2) does not existCf'(2) exist but f'(1) does not existDboth f'(1) and f'(2) exist
Draw the graph of the function: f(x)=|1−x|+|1+x|,−2≤x≤2
View SolutionIf a function f(x) is defined as f(x)=⎧⎪⎨⎪⎩−x,x<0x2,0≤x≤1x2−x+1,x>1 then
View SolutionLet f(x)={xfor0≤x<13−xfor1≤x≤2
Then f(x) is
View Solutionf (x) is an even periodic function with period 10 In [0,5],f(x)=⎧⎪⎨⎪⎩2x0≤x<23x2−82≤x<410x4≤x≤5. Then:
View SolutionIf f(x)=⎧⎨⎩x, for 0≤x<121−x, for 12≤x<1 , then
View Solution

