A line is drawn perpendicular to line y=5x, meeting the coordinate axes at AandB . If the area of triangle OAB is 10 sq. units, where O is the origin, then the equation of drawn line is 3x−y−9 (b) x−5y=10 x+4y=10 (d) x−4y=10
12
-12
10
-10
The correct Answer is:A, B
Let the equation of line be xa+yb=1.
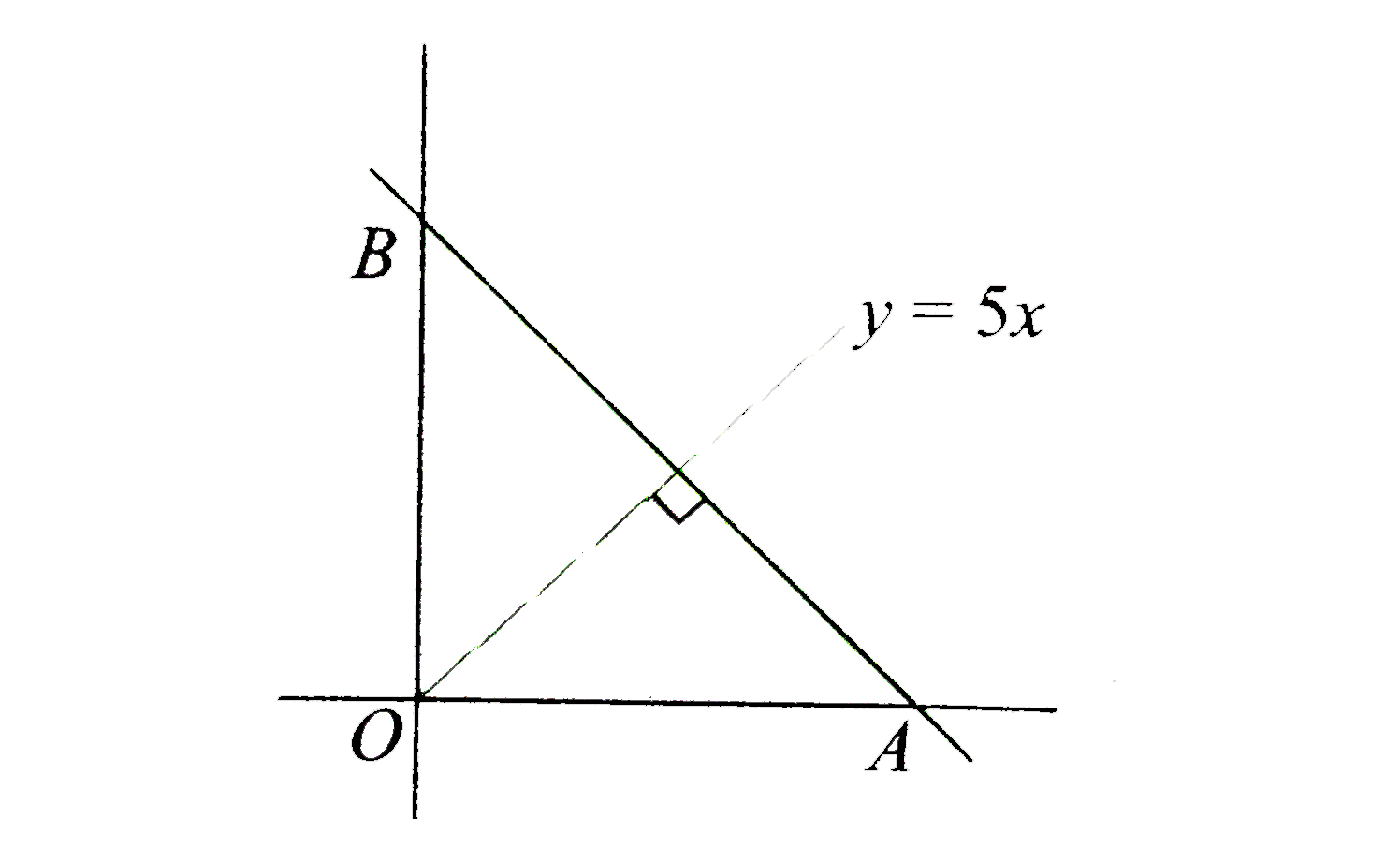
AB is perpendicular to y = 5x.
∴−ba×5=−1 or 5b=a
Area of ΔOAB=12|ab|
⇒10=12∣∣5b2∣∣
⇒b2=4
⇒b=±2
When b=2, a=10 " and when" b =-2, a=-10.
The line can be x10+y2=1 or x10+y2=−1.
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Comprehension)
27 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Matrix)
8 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Single)
82 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
A line is drawn perpendicular to line y=5x, meeting the coordinate axes at AandB . If the area of triangle OAB is 10 sq. units, where O is the origin, then the equation of drawn line is 3x−y−9 (b) x−5y=10 x+4y=10 (d) x−4y=10
View SolutionIf a line is perpendicular to the line 5x−y=0 and forms a triangle with coordinate axes of area 5 sq. units, then its equation is :
View Solution
Knowledge Check
The line 3x+4y−24=0 cuts the x -axis at A and y-axis at B. Then the increntre of a triangle OAB, where O is the origin is
A(1,2)B(2,2)C(12,2)D(2,12)The line 3x+4y−24=0 cuts the x -axis at A and y-axis at B. Then the increntre of a triangle OAB, where O is the origin is
A(1,2)B(2,2)C(12,12)D(2,12)Line L is perpendicular to the lines 5x−y=1. The area of triangle formed by the line and coordinate axes is 5. Its equation is
Ax+5y=√2Bx+5y=5√2Cx−5y=5√2Dx+5y=−√2
The line 7x+4y=28 cuts the coordinate axes at A and B. If O is the origin, then the ortho-centre of OAB is
View SolutionThe line 3x+4y−12=0 meets the corrdinates axes at A and B. Find the equation of the circle drawn of AB as diameter.
View SolutionIf a straight line perpendicular to 3x−4y−6=0 forms a triangle with the coordinate axes whose area is 6 sq. units, then the equation of the straight line (s) is
View SolutionLine L is perpendicular to the lines 5x−y=1. The area of triangle formed by the line and coordinate axes is 5. Its equation is
View SolutionThe line 3x + 4y - 24 = 0 intersects the X - axis at A and Y-axis at B . Then the Circumcentre of the ΔOAB , where O is the origin is
View Solution

