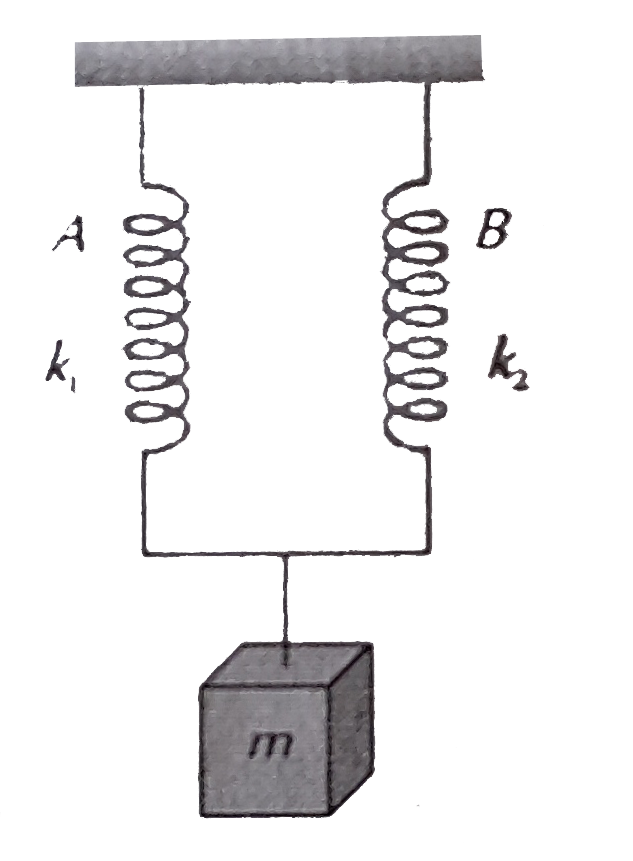
Two springs are joined and attached to a mass of 16 kg. The system is then suspended vertically from a rigid support. The spring constant of the two spring are k1andk2 respectively. The period of vertical oscillations of the system will be
8π√k1+k2k1k2
π2√k1k2
√k1+k28π
π√k1−k22
The correct Answer is:A
To solve the problem of finding the period of vertical oscillations of a mass attached to two springs in series, we can follow these steps:
Step 1: Understand the System
We have a mass m=16kg attached to two springs with spring constants k1 and k2. The springs are connected in series.
Step 2: Find the Equivalent Spring Constant
When two springs are connected in series, the equivalent spring constant kequiv can be calculated using the formula:
1kequiv=1k1+1k2
This can be rearranged to:
kequiv=k1k2k1+k2
Step 3: Write the Equation of Motion
When the mass is displaced from its equilibrium position, the forces acting on it are the weight of the mass mg acting downwards and the spring force kequivx acting upwards. The equation of motion can be written as:
ma=mg−kequivx
Where a is the acceleration and x is the displacement from the equilibrium position.
Step 4: Apply Newton's Second Law
Using Newton's second law, we can express the acceleration a as d2xdt2:
md2xdt2=mg−kequivx
This simplifies to:
d2xdt2=g−kequivmx
Step 5: Identify the Oscillation Equation
The above equation can be rearranged to resemble the standard form of simple harmonic motion:
d2xdt2+kequivmx=g
The term kequivm represents the angular frequency squared ω2.
Step 6: Find the Period of Oscillation
The period T of the oscillation is given by:
T=2π√mkequiv
Substituting kequiv into the equation:
T=2π
⎷mk1k2k1+k2
This simplifies to:
T=2π√m(k1+k2)k1k2
Step 7: Substitute the Mass
Now, substituting m=16kg:
T=2π√16(k1+k2)k1k2=8π√k1+k2k1k2
Final Result
Thus, the period of vertical oscillations of the system is:
T=8π√k1+k2k1k2
We have a mass m=16kg attached to two springs with spring constants k1 and k2. The springs are connected in series.
When two springs are connected in series, the equivalent spring constant kequiv can be calculated using the formula:
1kequiv=1k1+1k2
This can be rearranged to:
kequiv=k1k2k1+k2
When the mass is displaced from its equilibrium position, the forces acting on it are the weight of the mass mg acting downwards and the spring force kequivx acting upwards. The equation of motion can be written as:
ma=mg−kequivx
Where a is the acceleration and x is the displacement from the equilibrium position.
Using Newton's second law, we can express the acceleration a as d2xdt2:
md2xdt2=mg−kequivx
This simplifies to:
d2xdt2=g−kequivmx
The above equation can be rearranged to resemble the standard form of simple harmonic motion:
d2xdt2+kequivmx=g
The term kequivm represents the angular frequency squared ω2.
The period T of the oscillation is given by:
T=2π√mkequiv
Substituting kequiv into the equation:
T=2π
⎷mk1k2k1+k2
This simplifies to:
T=2π√m(k1+k2)k1k2
Now, substituting m=16kg:
T=2π√16(k1+k2)k1k2=8π√k1+k2k1k2
Thus, the period of vertical oscillations of the system is:
T=8π√k1+k2k1k2
Similar Questions
Knowledge Check
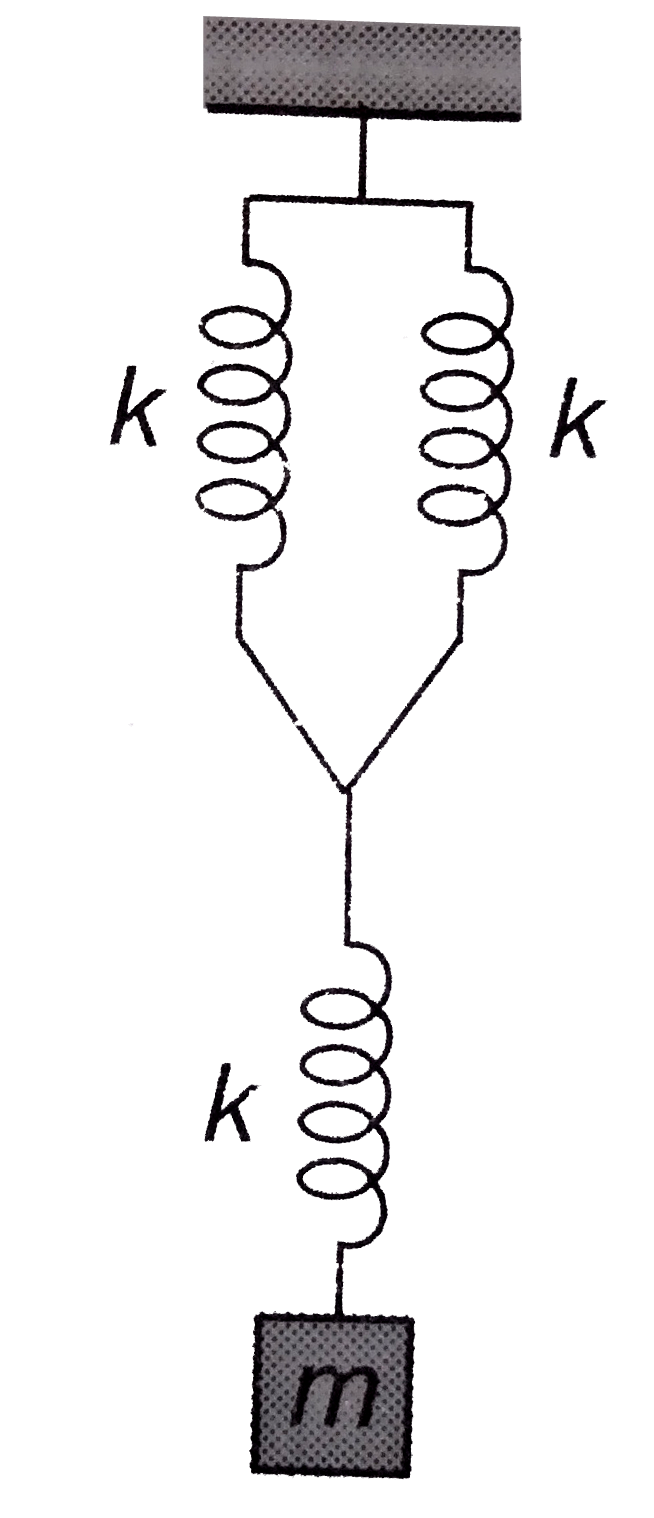
A particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mkA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mkA mass m is suspended by means of two coiled springs which have the same length in unstretched condition as shown in figure. Their force constants are k1andk2 respectively. When set into vertical vibrations, the period will be
 A2π√(mk1k2)B2π√m(k1k2)C2π√(mk1−k2)D2π√(mk1+k2)
A2π√(mk1k2)B2π√m(k1k2)C2π√(mk1−k2)D2π√(mk1+k2)
A mass m is suspended from the two coupled springs connected in series. The force constant for springs are k1andk2. The time period of the suspended mass will be
View SolutionA mass m is suspended from the two coupled springs connected in series. The force constant for spring are k1 and k2. The time period of the suspended mass will be:
View SolutionA mass m is suspended by means of two coiled spring which have the same length in unstretched condition as in figure. Their force constant are k 1 and k 2 respectively. When set into vertical vibrations, the period will be
View SolutionThe frequency of vertical oscillations of the three spring-mass system, shown in figure, is
View SolutionTwo particles (A) and (B) of equal masses are suspended from two massless spring of spring of spring constant k1 and k2, respectively, the ratio of amplitude of (A) and (B) is.
View Solution
