An object of mass m1 moving with speed v collides with another object of mass m2 at rest and stick to it. Find the impulse imparted to the second object.
To solve the problem of finding the impulse imparted to the second object after a collision, we can follow these steps:
Step 1: Understand the scenario
We have two objects:
- Object 1 with mass m1 moving with speed v.
- Object 2 with mass m2 at rest.
When these two objects collide, they stick together.
Step 2: Apply the principle of conservation of momentum
Since there are no external forces acting on the system, we can use the conservation of momentum. The total momentum before the collision must equal the total momentum after the collision.
Initial momentum (before collision):
- The momentum of object 1: Pinitial=m1⋅v
- The momentum of object 2 (at rest): Pinitial=0
Thus, the total initial momentum is:
Pinitial=m1⋅v+0=m1⋅v
Final momentum (after collision):
After the collision, both objects stick together and move with a common velocity v′. The total mass after the collision is m1+m2, so the final momentum is:
Pfinal=(m1+m2)⋅v′
Step 3: Set initial momentum equal to final momentum
Using conservation of momentum:
m1⋅v=(m1+m2)⋅v′
Step 4: Solve for the final velocity v′
Rearranging the equation to find v′:
v′=m1⋅vm1+m2
Step 5: Calculate the impulse imparted to the second object
Impulse is defined as the change in momentum. The impulse J imparted to object 2 can be calculated as:
J=Pfinal−Pinitial
Final momentum of object 2:
After the collision, the momentum of object 2 is:
Pfinal=m2⋅v′
Initial momentum of object 2:
Before the collision, the momentum of object 2 is:
Pinitial=0
Thus, the impulse on object 2 is:
J=m2⋅v′−0=m2⋅v′
Substituting v′ from Step 4:
J=m2⋅(m1⋅vm1+m2)
Final Answer
The impulse imparted to the second object is:
J=m1⋅m2⋅vm1+m2
---
We have two objects:
- Object 1 with mass m1 moving with speed v.
- Object 2 with mass m2 at rest.
Since there are no external forces acting on the system, we can use the conservation of momentum. The total momentum before the collision must equal the total momentum after the collision.
- The momentum of object 1: Pinitial=m1⋅v
- The momentum of object 2 (at rest): Pinitial=0
Pinitial=m1⋅v+0=m1⋅v
After the collision, both objects stick together and move with a common velocity v′. The total mass after the collision is m1+m2, so the final momentum is:
Pfinal=(m1+m2)⋅v′
Using conservation of momentum:
m1⋅v=(m1+m2)⋅v′
Rearranging the equation to find v′:
v′=m1⋅vm1+m2
Impulse is defined as the change in momentum. The impulse J imparted to object 2 can be calculated as:
J=Pfinal−Pinitial
After the collision, the momentum of object 2 is:
Pfinal=m2⋅v′
Before the collision, the momentum of object 2 is:
Pinitial=0
J=m2⋅v′−0=m2⋅v′
J=m2⋅(m1⋅vm1+m2)
The impulse imparted to the second object is:
J=m1⋅m2⋅vm1+m2
Similar Questions
An object of mass m1 collides with another object of mass m2, which is at rest. After the collision the objects move with equal speed in opposite direction. The ratio of the masses m2:m1 is
View SolutionAn object of mass m moving with speed u collides one dimentionally with another identical object at rest. Find their velocities after collision, if coefficient of restitution of collision is e.
View Solution
Knowledge Check
An object of mass M1 moving horizontally with speed u collides elastically with another object of mass M2 at rest. Select correct statement.
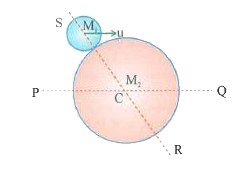 AThe momentum of system is conserved only in direction PQBMomentum of M1 is conserved in direction perpendicular to SRCMomentum of M2 will change in direction normal to CRDAll of these
AThe momentum of system is conserved only in direction PQBMomentum of M1 is conserved in direction perpendicular to SRCMomentum of M2 will change in direction normal to CRDAll of theseAn object of mass M1 moving horizontally with speed u collides elastically with another object of mass M2 at rest. Select correct statement.
 AThe momentum of system is consered only in direction PQBMomentum of M1 is conserved in direction perpendicular to SRCMomentum of M2 will change in direction normal to CRDAll of these
AThe momentum of system is consered only in direction PQBMomentum of M1 is conserved in direction perpendicular to SRCMomentum of M2 will change in direction normal to CRDAll of theseA ball of mass M moving with speed v collides perfectly inelastically with another ball of mass m at rest. The magnitude of impulse imparted to the first ball is
AMvBmvCMmM+mvDM2M+mv
A block of mass m moving at speed υ collides wilth another block of mass 2 m at rest. The lighter block comes to rest after the collision. Find the coefficient of restitution.
View SolutionAn object of mass m1 initially moving at speed v0 collides with an stationary abject of mass m2=αm1, where a<1. The collision could be completely elastic, completely inelastic, or partially inelastic. After the collision the two objects move at speeds v1 and v2. Assume that the collision is one dimensional , and that object one cannot pass through object two. After the collision, the speed ratio r1=v1/v0 of object 1 is bounded by
View SolutionA ball of mass m1 moving with a certain speed collides elastically with another ball of mass m2 kept at rest . If the first ball starts moving in reversed direction after the impact then
View SolutionA block of mass m moving with speed v , collides head on with another block of mass 2m at rest .
If coefficient of restitution is 12 then what is velocity of first block after the impact ?
View SolutionA ball of mass m moving at a speed v collides with another ball of mass 3m at rest. The lighter block comes to rest after collisoin. The coefficient of restitution is
View Solution
