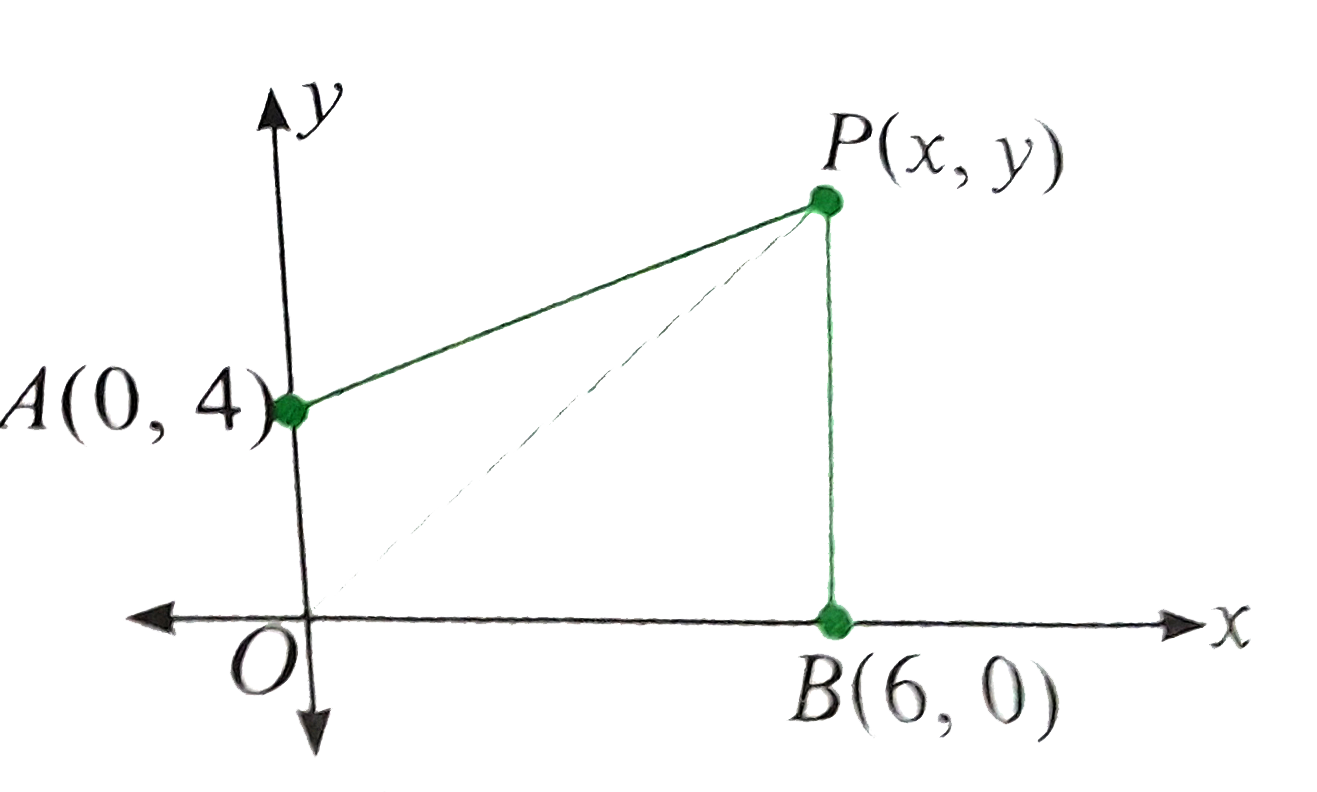
Let 0≡(0,0),A≡(0,4),B≡(6,0). Let P be a moving point such that the area of triangle POA is two times the area of triangle POB . The locus of P will be a straight line whose equation can be x+3y=0 (b) x+2y=0 2x−3y=0 (d) 3y−x=0
x+3y=0
x+2y=0
2x−3y=0
3y−x=0
The correct Answer is:A, D
Let point P be (x,y).
arΔPOA=12(OA)|x|=2|x|
arΔPOA=12(OB)|y|=3|y|
∴2|x|=6|y|
or |x|=3|y| or 3y−x=0or3y+x0
Similar Questions
The area of the triangle formed by the lines x + y - 3 = 0, x - 3y + 9 = 0 and 3x - 2y + 1 = 0 is -
View SolutionO(0,0),A(4,0),B(0,6) are the points. If P is a point such that the area of ΔPOB is twice the area of ΔPOA, then the locus of P is
View SolutionThe lines 2x + 3y-1 = 0, x + 2y-1 = 0 and ax + by -1 = 0 form a triangle whose perpendicular point is, then the value of (a, b) is
View SolutionThe coordinates of three points O, A, B are (0, 0), (0,4) and (6, 0) respectively. A point P moves so that the area of ΔPOA is always twice the area of ΔPOB. Find the equation to both parts of the locus of P.
View SolutionLet 0≡(0,0),A≡(0,4),B≡(6,0). Let P be a moving point such that the area of triangle POA is two times the area of triangle POB . The locus of P will be a straight line whose equation can be
View SolutionThe coordinates of three points O, A, B are (0, 0), (0,4) and (6, 0) respectively. A point P moves so that the area of ΔPOA is always twice the area of ΔPOB. Find the equation to both parts of the locus of P.
View SolutionIf the straight lines 2x+3y-1=0,x+2y-1=0,and ax+by-1=0 form a triangle with the origin as orthocentre, then (a , b) is given by
View SolutionLet 0-=(0,0),A-=(0,4),B-=(6,0)dot Let P be a moving point such that the area of triangle P O A is two times the area of triangle P O B . The locus of P will be a straight line whose equation can be
View Solution

