दो कण जिनके वेग सदिश क्रमश: (ˆi+ˆj+ˆk)
तथा (2ˆi+2ˆj+2ˆk) मी. / से हैं , द्विकन निकाये का निर्माण करते हैं । कणों के द्रव्यमान क्रमश: 1 किग्रा व 2 किग्रा हैं । कण तंत्र का द्रव्यमान केंद्र के सापेक्ष कुल रेखीय संवेग ज्ञात कीजिए ।
द्रव्यमान केंद्र का वेग
−−→Vcm=1(ˆi+ˆj+ˆk)+2(ˆi+2ˆj+2ˆk)1+2
या −−→Vcm=5ˆi+5ˆj+5ˆk3
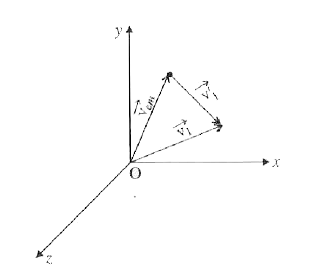
यदि किसी i वे कण का द्रव्यमान केंद्र के सापेक्ष वेग →V1 हो तथा मूल बिंदु के सापेक्ष V1 हो तो चित्र से
→V1=→V1−−−→Vcm
अतः →V1=(ˆi+ˆj+ˆk)−(5ˆi+5ˆj+5ˆk3)
या →V1=3ˆi+3ˆj+3ˆk−5ˆj−5ˆj−5ˆk3
→V1=−2ˆi−2ˆj−2ˆk3
इसी प्रकार →v2=(2ˆi+2ˆj+2ˆk)−(5ˆi+5ˆj+5ˆk3)
या →V2=ˆi+ˆj+ˆk3
अतः द्रव्यमान केंद्र के सापेक्ष कणों का कुल रेखीय संवेग
→P=m1→V1+m2→V2
=1×(−2ˆi−2ˆj−2ˆk3)+2(ˆi+ˆi+ˆk3)
=−2ˆi−2ˆj−2ˆk+2ˆi+2ˆj+2ˆk3
या →P=0
Similar Questions
बिंदु (a,b,c) से जाने वाले तथा तल ¯r.(ˆi+ˆj+ˆk)=2 के समांतर ताल का समीकरण ज्ञात कीजिए।
View SolutionIf 3ˆi+6ˆj+2ˆk,ˆi−2ˆj+3ˆkand5ˆi+2ˆj+mˆk are coplanar.
View Solutionमाना √3ˆi+ˆj,ˆi+√3ˆj तथा βˆi+(1−β)ˆj क्रमश: तीन बिन्दुओ A,B तथा C के मूलबिंदु O के सापेक्ष, स्थिति सदिश है । यदि C की, OA तथा OB के बीच बने न्यूनकोण के समद्विभाजक से दुरी 3√2 है, तो β के सभी संभावित मानो का योग है
View Solutionμ के उन भिन्न वास्तविक मानो का योग, जिनके लिए सदिश μˆi+ˆj+ˆk,ˆi+μˆj+ˆk तथा ˆi+ˆj+μˆk समतलीय (co-planar) है, है
View Solutionबिन्दु, जिनके स्थिति सदिश 60ˆi+3ˆj,40ˆi−8ˆj तथा aˆi−52ˆj हैं, सरेखीय होंगे। यदि
View Solutionλ का मान, यदि सदिश ˆi−3ˆj+ˆk,2ˆi+λˆj+ˆk तथा 3ˆi+ˆj−2ˆk एक समतल में हों, होगा
View Solutionउस गोले का सदिश समीकरण ज्ञात कीजिए जिसका केन्द्र (ˆi+2ˆj−3ˆk) तथा त्रिज्या 5 है।
View SolutionProve that point ˆi +2ˆj - 3ˆk ,2ˆi - ˆj + ˆk and 2ˆi + 5ˆj - ˆk from a triangle in space.
View Solution
