A spherical body of density ρ is floating half immersed in liquid of density d, if α is the surface tension of the liquid, then the diameter of the body is
√3αg(2ρ−d)
√6σg(2ρ−d)
√4σg(2p−d)
√12σg(2ρ−d)
The correct Answer is:A
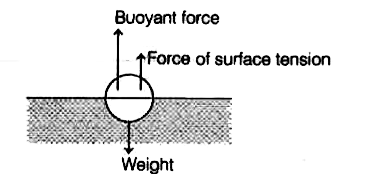
weight of body
= Bouyant force + Force of suface tension
43πr3ρ×g=23πr3dg+2πrδ
23πr3g(2ρ−d)=2πα
So,r2=3αg(ρ2p−d)
So, r=√3αg(2ρ−d)
Similar Questions
When a body of density rho and volume V is floating in a liquid of density sigma
View SolutionDrops of a liquid of density D surface tension T are floating in a liquid of density 'd' with half of the drop in the liquid, then the radius of the drop is :
View SolutionDrops of liquid of density d are floating half immersed in a liquid of density rho . If the surface tension of liquid is T then the radius of the drop will be (d = density of liquid drop)
View SolutionA drop of liquid of density rho is floating half-immersed in a liquid of density d. If sigma is the surface tension, then what is the diameter of the drop of the liquid ?
View SolutionDrops of liquid of density d are floating half immersed in a liquid of density ρ. If the surface tension of liquid is T then the radius of the drop will be (d = density of liquid drop)
View SolutionDrops of liquid of density d are floating half immersed in a liquid of density rho . If the surface tension of liquid is T then the radius of the drop will be (d = density of liquid drop)
View SolutionA drop of liquid of density rho is floating half-immersed in a liquid of density d. If sigma is the surface tension, the diameter of the drop of the liquid is :
View SolutionA body of density rho is immersed in a liquid of density rho_(L) .State condition when the body will (i) float (ii) sink in liquid.
View Solution

