In a spherical glass marble of radius 6 cm, a small air bubble is formed at 1 cm from the centre of the marble. The apparent position of the air bubble from the nearest point on the surface of the marble is about,
(refractive index of glass is 1.5.)Solution in Telugu
3.3 cm
4.6 cm
5.4 cm
7.0 cm
The correct Answer is:A
Refractive index of glass,
μ=Real distance(d1)Apparent distance(d2)
Given, d1=(6−1)cm=5cm
or 1.5=5d2 (∵μ=1.5, given )
or d2=3.33cm
Similar Questions
6 cm त्रिज्या तथा 1.5 अपवर्तनांक वाले एक काँच के गोले में हवा का एक छोटा बुलबुला, यदि इसमें से होकर गुजरनेवाले व्यास की और से देखा जाए, तो पास वाली सतह से 2 cm पर मालूम पड़ता है। बुलबुले की वास्तविक स्थिति ज्ञात करे।
View Solutionकाँच के 7 सेमी त्रिज्या वाले एक ठोस काँच के गोले के अन्दर हवा का एक बुलबुला है, जो त्रिज्या की दिशा में देखने पर गोले की सतह से 5.6 सेमी दूर दिखाई देता है। यदि काँच का अपवर्तनांक 1.5 हो, तो हवा के बुलबुले की वास्तविक स्थिति ज्ञात कीजिए।
View Solutionकाँच के एक गोले की त्रिज्या 3 सेमी है। उसके अन्दर गोले के केन्द्र से 1 सेमी की दूरी पर वायु का एक बुलबुला है। यदि काँच का अपवर्तनांक 1.5 है, तो (i) बुलबुला के निकट वाले पृष्ठ से देखने पर, (ii) बुलबुले के दूर वाले पृष्ठ से देखने पर वह कितनी दूर दिखाई देगा ?
View SolutionA spherical solid glass paper weight of diameter 6 cm has a small air bubble at a distance of 1.5 cm from the centre. If the air bubble be viewed from the side to which it is nearest along the line joining the bubble and the centre, find where will it appear.
View SolutionThere is a small air bubble inside a glass sphere (μ=1.5) of radius 10 cm. The bubble is 4 cm below the surface and is viewed normally from the outside. The apparent depth of the bubble is
View SolutionThere is a small air bubble inside a glass sphere (μ=1.5) of radius 10 cm. The bubble is 4.0cm below the surface and is viewd normally from the outside. Find the apparent dipth of the bubble.
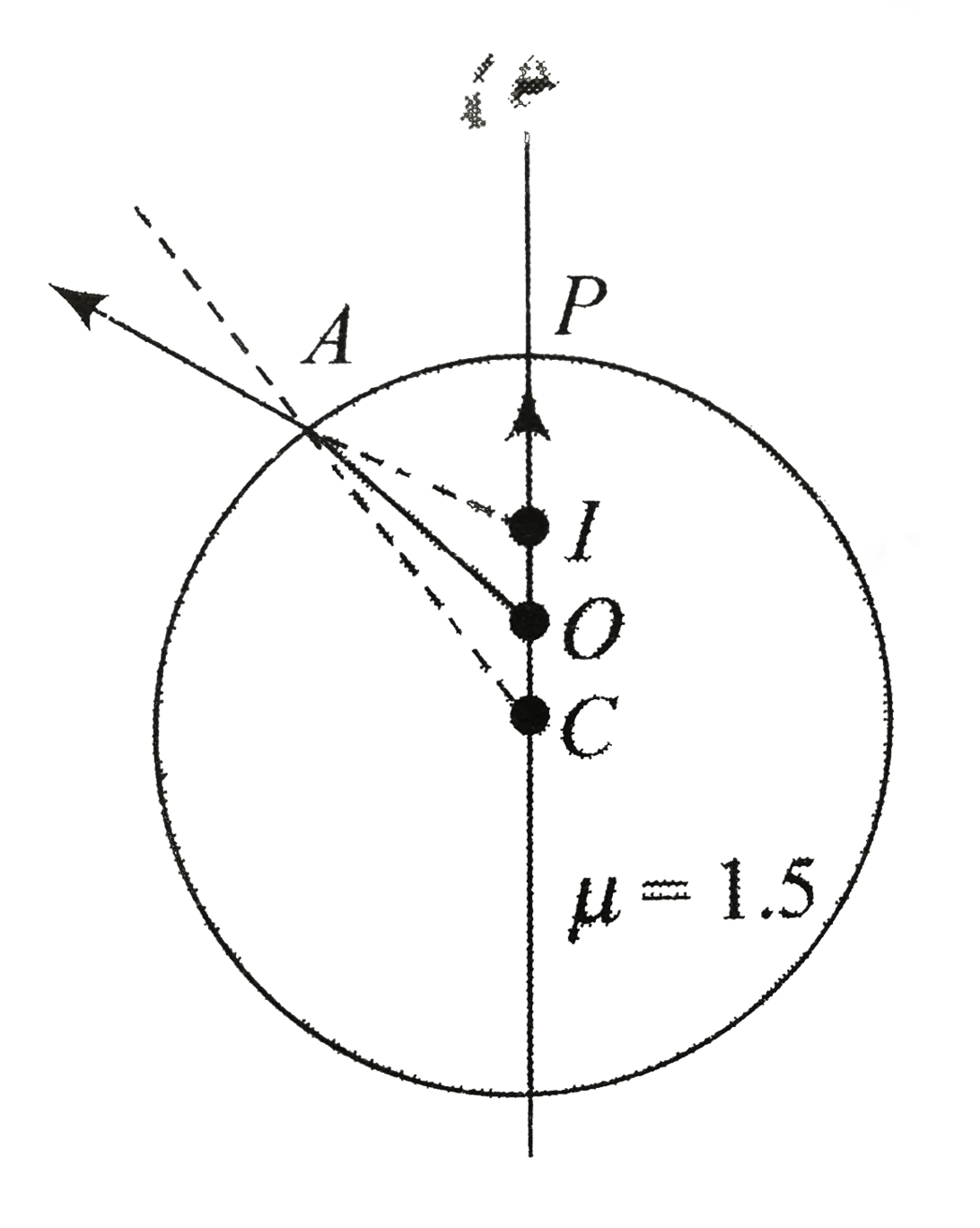
View SolutionThere is a small air bubble at the centre of a solid glass sphere of radius r and refractive index μ. What will be the apparent distance of the bubble from the centre of the sphere, when viewed from outside?
View Solution
