There is a point object at a height h above the surface of water in a tank. If the bottom of the tank acts as a plane mirror where will be the image formed? If an observer looks from air at the surface of water normally, calculate the distance of the image from that surface of water of the tank formed by the mirror-like bottom surface of the tank. Refractive index of water =43.
Q is a point source. For refraction in water the apparent position of Q is Q. [Fig. 2.57].
So, μ=apparent heightreal height=PQ.PQ
=PQ.h
or, PO.=μh=43h
Therefore the distance of Q. from the bottom of the tank
=d+43h
So the image of Q. will be formed at a distance of (d+43h) from the bottom of the tank.
The distance of the image from the surface of water
=d+d43h=2d+43h
If the apparent distance of the image from the surface of water the eye of an observe in air medium is x then,
43=2d+43hx
or, x=43(2d+43h)=32d+h

Topper's Solved these Questions
- REFRACTION OF LIGHTBook:CHHAYA PUBLICATIONChapter:REFRACTION OF LIGHTExercise:HIGHER ORDER THINKING SKILL (HOTS QUESTION)
Explore 25 Videos
- REFRACTION OF LIGHTBook:CHHAYA PUBLICATIONChapter:REFRACTION OF LIGHTExercise:SECTION RELATED QUESTION
Explore 18 Videos
- REFLECTION OF LIGHTBook:CHHAYA PUBLICATIONChapter:REFLECTION OF LIGHTExercise:INTEGER ANSWER TYPE
Explore 3 Videos
- SEMICONDUCTORS AND ELECTRONICS Book:CHHAYA PUBLICATIONChapter:SEMICONDUCTORS AND ELECTRONICS Exercise:CBSE SCANNER
Explore 31 Videos
Similar Questions
A concave mirror of radius of curvature one meter is placed at the bottom of a tank of water. The mirror forms an image of the sun when it is directly overhead. Calculate the distance of the images from the mirror for (a) 80cm and (b) 40cm of water in the tank ( μ=4/3 for water)
View SolutionA tank is filled to a height H. The range of water coming out of a hole which is a depth H/4 from the surface of water level is
View Solution
Knowledge Check
There is a hole h metre from its top of a tank filled with water. Calculate the distance x where the stream of water will touch the ground from the bottom (in m).
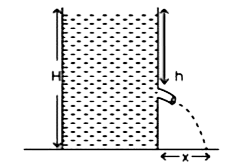 A2√h(H−h)B2√g(H−h)C√2hHD√2gH
A2√h(H−h)B2√g(H−h)C√2hHD√2gHTwo holes are made in the side of the tank such that the jets of water flowing out of them meet at the same point on the ground. If one hole is at a height of 3cm above the bottom, then the distance of the other holes from the top surface of water is
A32cmB√6cmC√3cmD3cmA tank is filled to a height H. The range of water coming out of a hole which is a depth H/4 from the surface of water level is
A2H√3B√3H2C√3HD3H4
A tank cotaining water has an orifice 10 m below the surface of water in the tank . If there is no wastage of energy ,find the speed of discharge.
View SolutionA convex lens is held 45cm above the bottom of an empty tank. The image of a point at the bottom of a tank is formed 36cm above the lens. Now, a liquid is poured into the tank to a depth of 40cm. It is found that the distance of the image of the same point on the bottom of the tank is 48cm above the lens. Find the refractive index of the liquid.
View SolutionThe height of the water in a tank is H. The range of the liquid emerging out from a hole in the wall of the tank at a depth 3H4 from the upper surface of water, will be
View SolutionThe height of the water in a tank is H. The range of the liquid emerging out from a hole in the wall of the tank at a depth 3H4 from the upper surface of water, will be
View SolutionA man stnading in a swimming pool looks at a stone lying at the bottom. The depth of the swimming pool is h. At what distance from the surface of water is the image of the stone formed? (Line of vision is normal, Refractive index of water is n)
View Solution

