prove that the diagonals of a rhombus are perpendicular to each other. Solution in Bengali
Video Solution
Text Solution
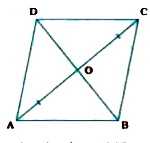
In Fig. 2.54 , ABCD is a rhombus. −−→AB=−−→DC=→aand−−→AD=−−→BC=→b, the values of →aand→b are the same for a rhombus.

Let a=b=m
−−→AC=−−→AB+−−→BC=→a+→b
and −−→BD=−−→BA+−−→AD=−→a+→b
∴→AC⋅→BD=(→a+→b)⋅(−→a+→b)=−→a⋅→a+→a⋅→b−→b⋅→a+→b⋅→b
=−a2+→a⋅→b−→a⋅→b+b2=−m2+m2=0
As the dot product is 0, the angle between the vector =90∘, i.e., −−→ACand−−→BD are perpendicular to each other.
|
Topper's Solved these Questions
Similar Questions
Distinguish between scalar and vector quantities.
View SolutionShow that the diagonals in the rhombus are perpendicular to each other.
View SolutionShow that the diagonals of a rhombus are perpendicular to each other
View SolutionUsing analytical geometry, prove that the diagonals of a rhombus are perpendicular to each other.
View SolutionShow that the diagonals of a rhombus are perpendicular to each other
View SolutionUsing analytical geometry, prove that the diagonals of a rhombus are perpendicular to each other.
View SolutionShow that the diagonals of a rhombus are perpendicular to each other.
View Solution

