Find the velocity of the centre of mass of two identical particles moving with velocities v1 and v2. Solution in Bengali
If the mass of each particle is m, the resultant momentum = (m→v1+m→v2)=m(→v1+→v2). If the velocity of the centre of mass of the two particles is →r, then the momentum of the centre of mass = (m+m) →r=2m→v.
∴ 2m→v=m(→v1+→v2)
Hence →v=→v1+→v22
Topper's Solved these Questions
Similar Questions
A large number of particles are placed around the origin each at a distance R from the origin. The distance of the centre of mass of the system from the origin is
View SolutionTwo particles are moving with velocities v_(1) and v_2 . Their relative velocity is the maximum, when the angle between their velocities is
View SolutionTwo identical particles move towards each other with velocity 2 v and v respectively. The velocity of centre of mass is
View Solutionसमान द्रव्यमान के दो पिंड v1 और v2 वेग से एक ही रेखा में गतिमान हैं । उनके मध्य प्रत्यास्थ संघट्ट होता है । संघट्ट के पश्चात उसके वेग हो जायेंगे -
View SolutionIn the figure block moves downwards with velocity v1, the wedge rightwards with velocity v2. The correct relation between v1 and v2 is
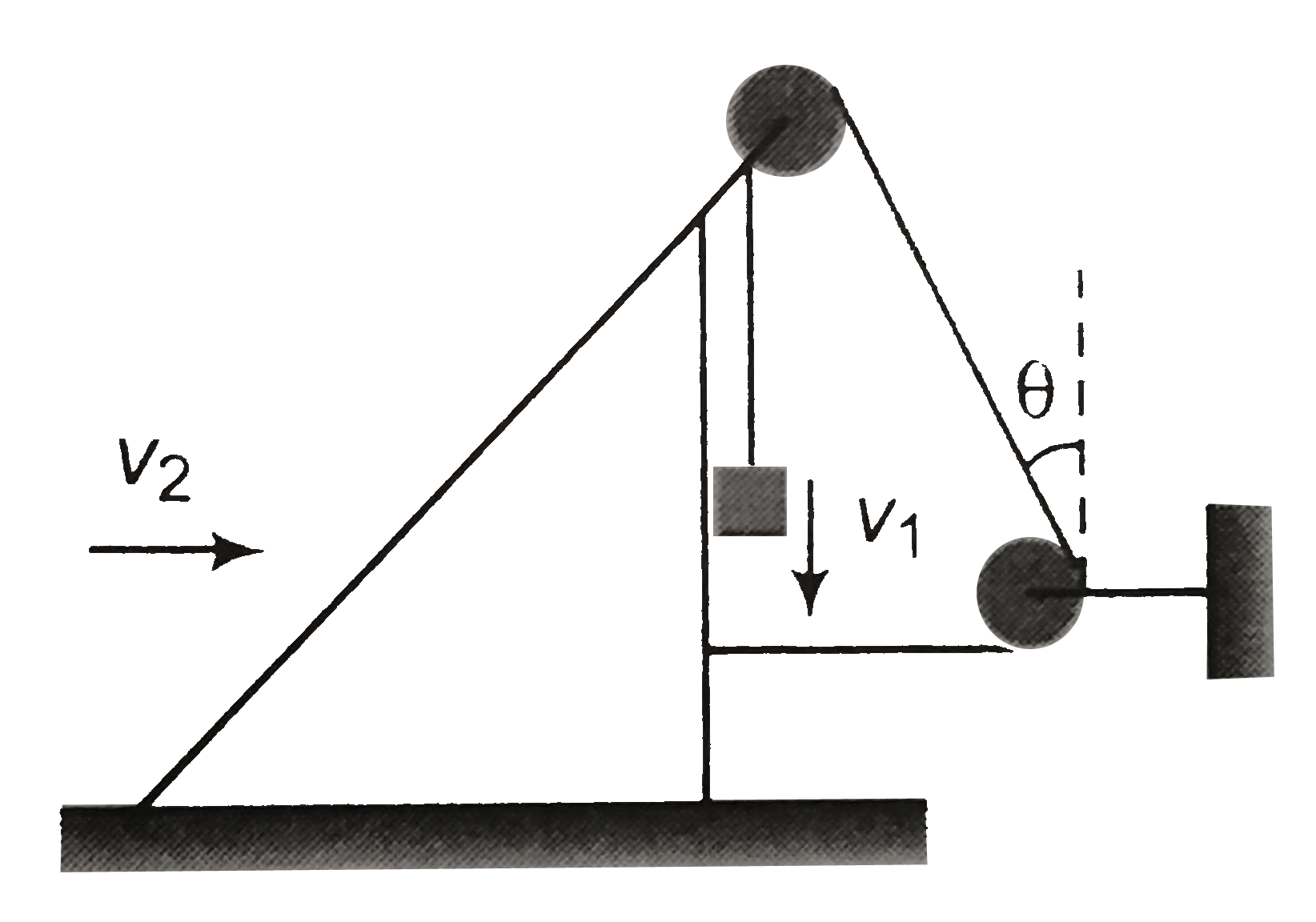
View SolutionA particle of mass m is moving with a uniform velocity v_(1) . It is given an impulse such that its velocity becomes v_(2) . The impulse is equal to
View SolutionIn fig., blocks A and B move with velocities v_(1) and v_(2) along horizontal direction. Find the ratio of v_(1)//v_(2)
View Solution
