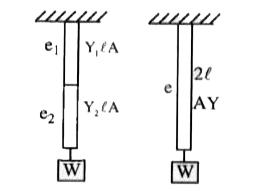
Two rods of different materials but of the same sectional area have lengths L1 and L2. IF their Young's moduli are Y1 and Y2 respectively. Then calculate the equivalent Young's modulus of the composite system when the two rods are joined along their lengths.Solution in Bengali
The correct Answer is:[Y1Y2(l1+l2)L1Y2+L2Y1]
Step by step video, text & image solution for Two rods of different materials but of the same sectional area have lengths L_1 and L_2. IF their Young's moduli are Y_1 and Y_2 respectively. Then calculate the equivalent Young's modulus of the composite system when the two rods are joined along their lengths. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The length of a metallic wire is l1 metre when the tension is 4 N and l2 metre when the tension is 6N respectively. Find the length when the tension is 9N and the actual length of the wire.
View SolutionA train standing at the outer singal of a railway station blows a whistle of frequency 400 Hz in still air. (i) What is frequency of the whistle for a platform observer when the train (a) approaches the platform with a speed of 10 m/s, (b) recedes from the platform with a speed of 10 m/s. (ii) What is the speed of sound in each case if the speed of sound in still air is 340 m/s.
View SolutionTwo rods of different metals having the same area of cross section A are placed between the two massive walls as shown is Fig. The first rod has a length l1, coefficient of linear expansion α1 and Young's modulus Y1. The correcsponding quantities for second rod are l2,α2 and Y2. The temperature of both the rods is now raised by t∘C.
i. Find the force with which the rods act on each other (at higher temperature) in terms of given quantities.
ii. Also find the length of the rods at higher temperature.

View SolutionTwo wires of equal length and cross sectional area suspended as shown in Their Young's modulii are Y_1 = 2xx10^(11) Pa and Y_2 = 0.90 xx 10^(11) Pa respectively. What will be the equivalent Young's modulus of combination?
View SolutionTwo wires of equal length and cross-sectional area are suspended as shown in figure. Their Young's modullare Y_1 and Y_2 respectively. The equivalent Young's modulil will bebr>
View SolutionYoung moduli of two rods of equal length and equal cross section and Y1 and Y2. These rods are joined end to end forming a composite rod-system. Prove that the equivalent Young's modulus of the composite system of rods =2Y1Y2Y1+Y2
View SolutionTwo rods of equal length and cross- sectional area have their Young's moduli Y_1 and Y_2 respectively. IF the rods are joined end to end, then the equivalent Young's modulus of the combined rod system is
View SolutionTwo wires A and B have the same length and area of cross-section. But Young's modulus of A is two times the Young's modulus of B. Then the ratio of force constant of A to that of B is
View SolutionTwo wires of same length and radius are joined end to end and loaded. The Young.s modulii of the materials of the two wires are Y1andY2. If the combination behaves as a single wire them its Young.s modulus is
View SolutionTwo rods of different metals having the same area of cross section A are placed between the two massive walls as shown is Fig. The first rod has a length l1, coefficient of linear expansion α1 and Young's modulus Y1. The correcsponding quantities for second rod are l2,α2 and Y2. The temperature of both the rods is now raised by t∘C.
i. Find the force with which the rods act on each other (at higher temperature) in terms of given quantities.
ii. Also find the length of the rods at higher temperature.

View SolutionTwo rods of identical dimensions with Young's modulus Y_1 and Y_2 are joined end to end. The equivalent Young's modulus for the composite rod is
View SolutionTwo wires of equal length and cross sectional area suspended as shown in Their Young's modulii are Y_1 = 2xx10^(11) Pa and Y_2 = 0.90 xx 10^(11) Pa respectively. What will be the equivalent Young's modulus of combination?
View SolutionTwo rods of different materials having coefficient of thermal expansion α1 and α2 and Young's modulus Y1 and Y2 respectively are fixed between two rigid supports separately. The rods are heated such that they undergo same temperature increment. If thermal stress developed in two rods are equal, then Y1:Y2 is
View SolutionTwo rods of different metals having the same area of cross section A are placed between the two massive walls as shown is Fig. The first rod has a length l_1 , coefficient of linear expansion alpha_1 and Young's modulus Y_1 . The correcsponding quantities for second rod are l_2,alpha_2 and Y_2 . The temperature of both the rods is now raised by t^@C . i. Find the force with which the rods act on each other (at higher temperature) in terms of given quantities. ii. Also find the length of the rods at higher temperature.
View SolutionTwo wires of equal length and cross sectional area suspended as shown in
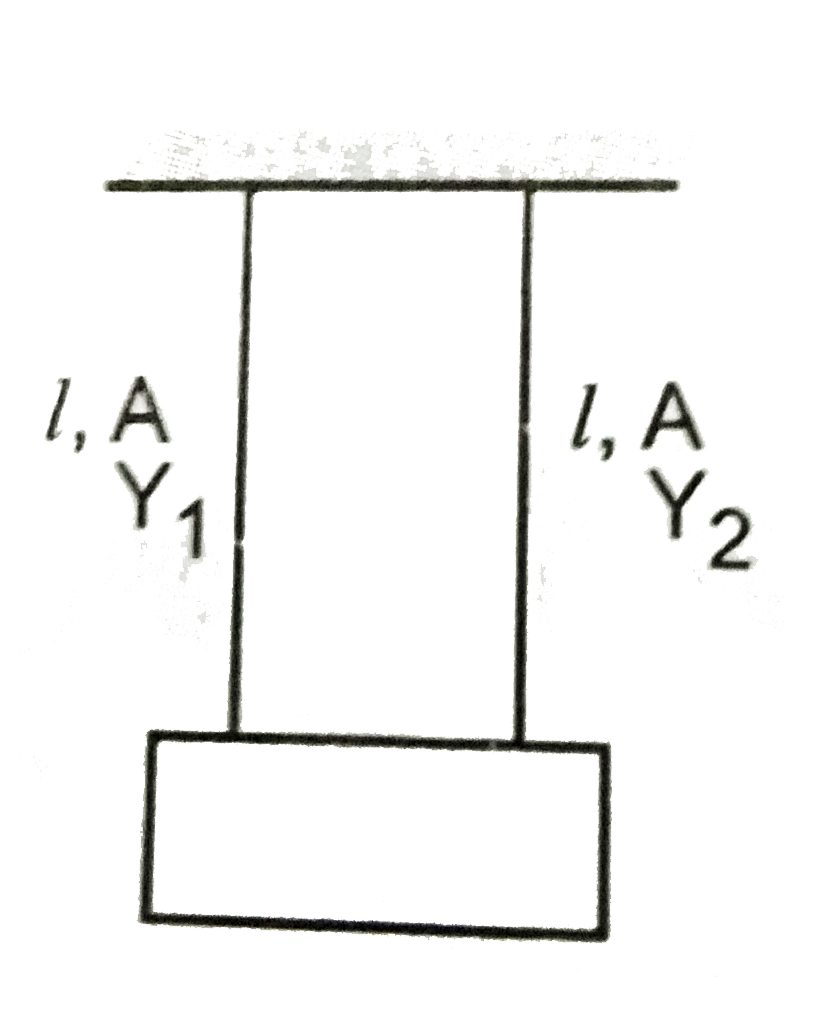
Their Young's modulii are Y1=2×1011 Pa and Y2=0.90×1011 Pa respectively. What will be the equivalent Young's modulus of combination?
View Solution

