A uniform rod of density ρ is placed in a wide tank containing a liquid of density ρ0(ρ0>ρ). The depth of liquid in the tank is half the length of the rod. The rod is in equilibrium, with its lower end resting on the bottom of the tank. In this position the rod makes an angle θ with the horizontal. Determine θ.
The correct Answer is:sin−1(12√ρ0ρ)
Topper's Solved these Questions
Similar Questions
A spring balance A reads 2 kg with a block suspended from it. Another balance B reads 5 kg when a beaker with liquid is put on the pan of the balance. When the block is immersed in water
View SolutionWhat would be the effect on the rms speed of gas molecules if the temperature of the gas is increased by a factor of 4?
View SolutionA uniform rod of length L rests against a smooth roller as shown in figure. Find the friction coefficient between the ground and the lower end if the minimum angle that rod can make with the horizontal is θ.

View SolutionFigure shown a container having liquid of variable density. The density of liquid veriesas rho=rho_(0)(4-(3h)/(h_(0))) . Here, h_(0) and rho_(0) are constants and h is measured from bottom of the container. A solid block of small dimensions whose density is (5)/(2) rho_(0) and mass m is released from bottom of the tank. Prove that the block will execute simple harmonic motion. Find the frequency of oscillation. .
View SolutionA uniform rod of length L rests against a smooth roller as shown in figure. Find the friction coefficient between the ground and the lower end if the minimum angle that rod can make with the horizontal is θ.

View SolutionA uniform rod of length L pivoted at the bottom of a pond of depth L//2 stays in stable equilibrium as shown in the figure. Find the angle 0 if the density of the material of the rod is half of the density of water.
View SolutionA uniform rod of density rho is placed in a wide tank containing a liquid of density rho_0 (rho_0 gt rho) . The depth of liquid in the tank is half the length of the rod. The rod is in equilibrium, with its lower end resting on the bottom of the tank. In this position the rod makes an angle theta with the horizontal.
View SolutionThe linear mass density i.e. mass per unit length of a rod of length L is given by ρ=ρ0(1+xL), where ρ0 is constant , x distance from the left end. Find the total mass of rod and locate c.m. from the left end.

View SolutionConsider a rod of length l resting on a wall and the floor. If the velocity of the upper end of a rod A is v_(0) in downward direction, find the velocity of the lower end B at this iinstant, when the rod makes an angle theta with horizontal
View SolutionA rod of length L and cross section area A has variable density according to the relation ρ(x)=ρ0+kx for 0≤x≤L2 and ρ(x)=2x2 for L2≤x≤L where ρ0 and k are constants. Find the mass of the rod.
View SolutionA liquid of density rho_0 is filled in a wide tank to a height h. A solid rod of length L, cross-section A and density rho is suspended freely in the tank. The lower end of the rod touches the base of the tank and h=L/n (where n gt 1). Then the angle of inclination theta of the rod with the horizontal in equilibrium position is
View SolutionAn insulting thin rod of length l has a linear charge density rho(x)=rho_(0)(x)/(l) on it. The rod is rotated about an axis passing through the origin (x=0) and perpendicular to the rod. If the rod makes n rotations per second, then the time averaged magnetic moment of the rod is :
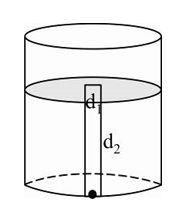
View SolutionA thin rod of length L and area of cross section S is pivoted at its lowest point P inside a stationary, homogeneous and non-viscous liquid. The rod is free to rotate in a vertical plane about a horizontal axis passing through P. The density d1of the rod is smaller than the density d2 of the liquid. The rod is displaced by a small angle theta from its equilibrium position and then released. Shown that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters ___________ .
View SolutionA ladder of length 5m is placed against a smooth wall as shown in figure. The coefficient or friction is μ between ladder and ground. What is the minimum value of μ , If the ladder is not to slip?

View SolutionAn insulting thin rod of length l has a linear charge density ρ(x)=ρ0xl on it. The rod is rotated about an axis passing through the origin (x=0) and perpendicular to the rod. If the rod makes n rotations per second, then the time averaged magnetic moment of the rod is :
View Solution

