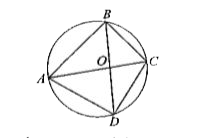
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD arediameters, (ii) ABCD is a rectangle
Video Solution
Text Solution
AC and BD are chords of circle.
anyline which is perpendicular and bisects the chord that line will pass through the centre.
BD=diameter and AC=diameter.
In∠AOBand∠DOC
OC=OA
OB=OD
∠AOB=∠DOC
∠AOB≅∠DOC
∠DAO=∠BCO
If alternate angle are equal AB||CD and AD||BC
ABCD is a cyclic quadrilateral
ABCD is a rectangle.
|
Similar Questions
Knowledge Check
If AC and BD are two chords of a circle that bisect each other then quadrilateral ABCD is a
 ArectangleBsquareCtrapeziumDparallelogram
ArectangleBsquareCtrapeziumDparallelogram
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD arediameters, (ii) ABCD is a rectangle
View SolutionACandBD are chords of a circle that bisect each other. Prove that:AC and BD are diameter. ABCD is a rectangle
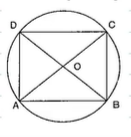
View SolutionIn the given figure AB and CD bisect each other at O. Prove that AC = BD.
View SolutionO is the centre of a circle. AC and BD are two chords of the circle intersecting each other at P, If ∠AOB=15∘and∠APB=30∘, then ∠COD is equal to
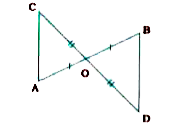
View SolutionTwo segments AC and BD bisect each other at O . Prove that ABCD is a parallelogram.
View SolutionIn the given figure, prove that AC=BD.

View SolutionDiagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar(ΔAOD) = ar(ΔBOC).
View Solution