If →A=3i+j+2k and →B=2i−2j+4k and θ is the angle between the two vectors, then sinθ is equal to
23
2√3
2√7
2√13
The correct Answer is:C
sinθ=∣∣¯¯¯Aׯ¯¯B∣∣AB
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - II (C.W)
Explore 60 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - II (H.W)
Explore 60 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - I (C.W)
Explore 63 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-VI
Explore 78 Videos
- THERMAL PROPERTIES OF MATTERBook:NARAYNAChapter:THERMAL PROPERTIES OF MATTERExercise:LEVEL - II (H.W.)
Explore 19 Videos
Similar Questions
A uniform wire is bent into the form of a rectangle of length L and width W. The coordinates of its centre of mass from a corner are
View SolutionFigure shows composite system of two uniform rods of length as indicated . Then the coordinates of the centre of mass of the system of rods are

View SolutionA system consists of two masses connected by a massless rod lies along x - axes . The distance of cnetre of mass from O is

View SolutionThe point P of a string is pulled up with an acceleration g. Then the acceleration of the hanging disc (w.r.t ground) over which the string is wrapped, is
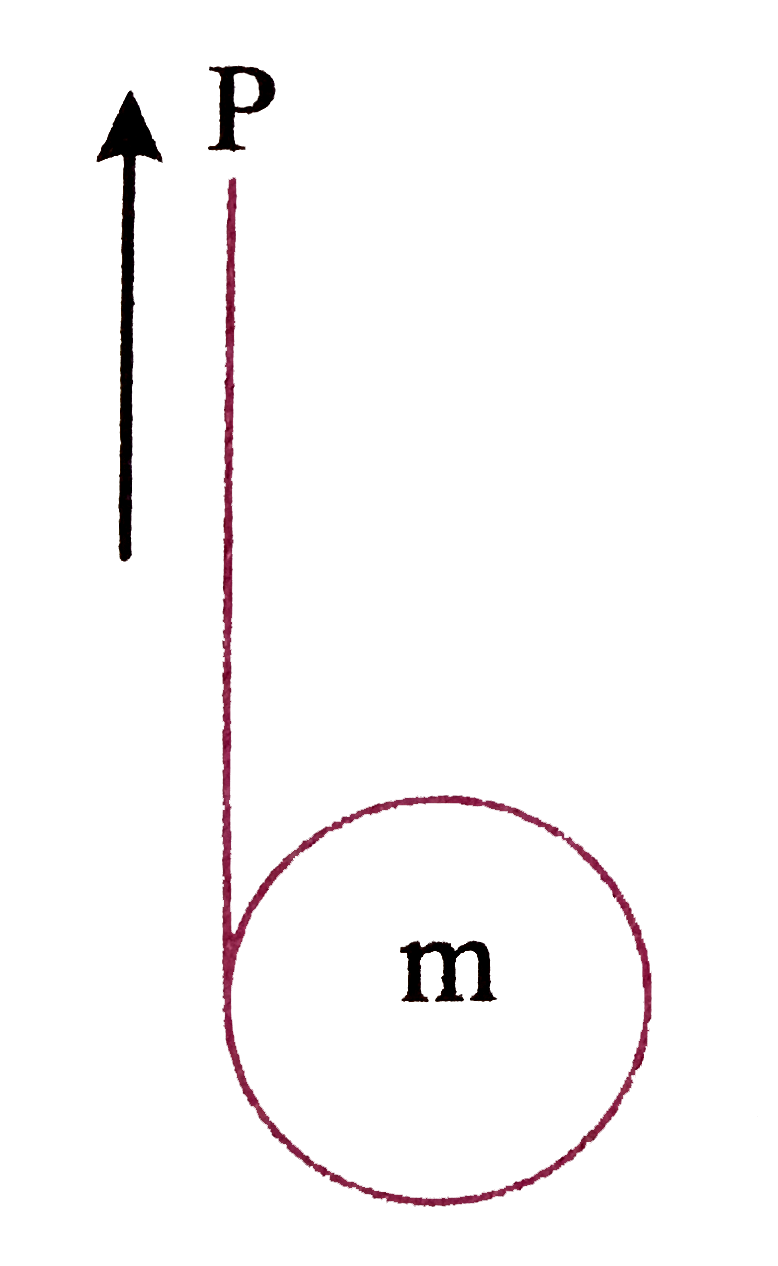
View SolutionThe ratio of coefficients of apparent expansions of the same liquid in two different vessels is 1:2. If α1 and α2 are the coefficient of linear expansions then coefficient of real expansion of the liquid is
View SolutionIf the vector →v with magnitude √6 is along the intemal bisector of the angle between →a=7i−4j−4k and →b=−2i−j+2k,then →v.→a equals
View SolutionFind an expression for the sine of the angle between the two vectors 3i+j+2k and 2i-2j+4k
View SolutionIf angle between two unit vectors vec a and vec b is theta then sin((theta)/(2)) is equal to
View SolutionIf →a=−→2i−→2j+−→4k,→b=−→2i+→4j−−→2kand→c=→4i−→2j−−→2k Calculate the value of [→a→b→c] and interpret the result.
View SolutionIf →A=3i+j+2k and →B=2i−2j+4k and θ is the angle between the two vectors, then sinθ is equal to
View SolutionIf →OA=i++k,→AB=3i−2j+k,→BC=i+2j−2k,→CD=2i+j+3k then the position vector of D is
View SolutionIf θ is th angle between the vector 2i - 2j + 4k and 3i + j + 2k, then sin θ =
View SolutionIf the position vector of A,B,C are 2i+3j+4k,i+2j,j+2kand −−→AB=P−−→AC then P=
View SolutionIf the position vector of A,B,C are 2i+3j+4k,i+2j,j+2kand −−→AB=P−−→AC then P=
View SolutionIf θ is the angle between any two vectors →a and →b , then ∣∣→a.→b∣∣=∣∣→a×→b∣∣, when θ is equal to
View Solutionयदि दो सदिश →a और →b के बीच का कोण θ है तो ∣∣→a.→b∣∣=∣∣→a×→b∣∣ जब θ बराबर है :
View Solution
