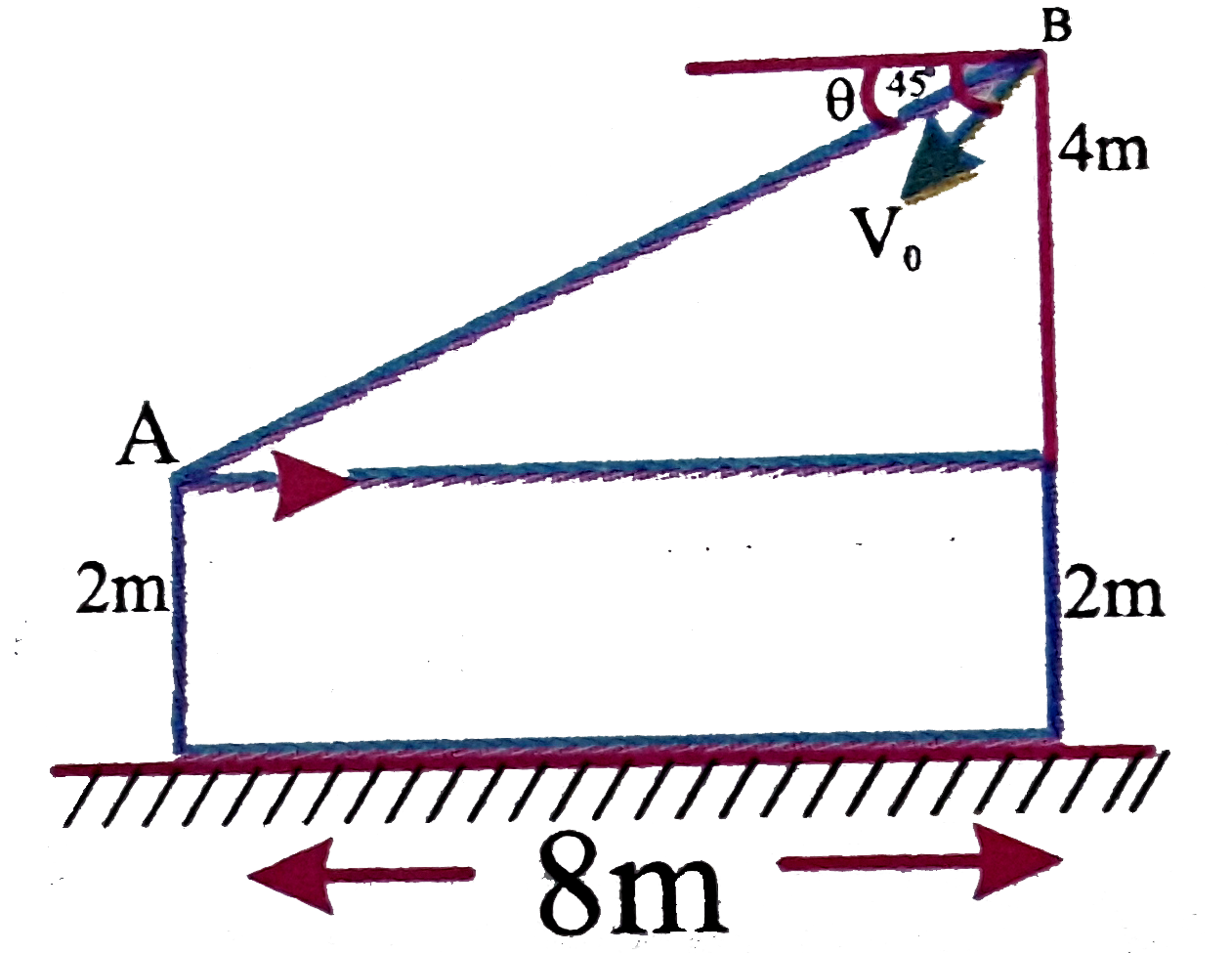
From points A and B, at the respective heights of 2m and 6m, two bodies are thrown simultaneouly towards each other, one is thrown horizontally with a velocity of 8ms and the other, downward at an angle 45∘ to the horizontal at an initial velocity v0 such that the bodies collide in flight. The horizontal distance between points A and B equal to 8m.Then find
The initial velocity V0 of the body thrown at an angle 45∘
The time of flight of the bodies before colliding
The coordinate (x,y) of the point of collision (consider the botton of the tower A as origin) is
To solve the problem step by step, we will follow the motion equations for both bodies and find the required values.
Step 1: Understand the Problem
We have two bodies thrown from points A and B. Body A is thrown horizontally from a height of 2 m with a velocity of 8 m/s, and body B is thrown downward at a 45-degree angle from a height of 6 m with an initial velocity V0.
Step 2: Set Up the Coordinate System
We will set the bottom of tower A (height = 0) as the origin (0, 0). Therefore:
- The height of point A = 2 m (coordinates: (0, 2))
- The height of point B = 6 m (coordinates: (8, 6))
Step 3: Determine the Time of Flight
Let t be the time taken for the bodies to collide. The horizontal distance traveled by body A is given by:
xA=8⋅t
For body B, which is thrown at a 45-degree angle, the horizontal distance is:
xB=V0⋅cos(45∘)⋅t=V0√2⋅t
Since the total horizontal distance between A and B is 8 m:
xA+xB=8
8t+V0√2t=8
Factoring out t:
t(8+V0√2)=8
Thus,
t=88+V0√2
Step 4: Set Up the Vertical Motion Equations
For body A (thrown horizontally):
The vertical position yA after time t is given by:
yA=2−12gt2
Where g=10m/s2.
For body B (thrown downward):
The vertical position yB after time t is:
yB=6−V0⋅sin(45∘)⋅t−12gt2=6−V0√2t−12gt2
Step 5: Set Up the Height Difference Equation
The difference in heights when they collide is:
yB−yA=4
Substituting the equations for yA and yB:
(6−V0√2t−12gt2)−(2−12gt2)=4
This simplifies to:
6−2−V0√2t=4
Thus:
4−V0√2t=4
This leads to:
−V0√2t=0
Step 6: Solve for V0
From the previous equation, we can isolate V0:
V0=8√2
Step 7: Calculate Time of Flight
Substituting V0 back into the time equation:
t=88+8√2√2=88+8=816=0.5s
Step 8: Find the Coordinates of Collision
For body A:
xA=8⋅t=8⋅0.5=4m
For the vertical position of body A at collision:
yA=2−12⋅10⋅(0.5)2=2−12⋅10⋅0.25=2−1.25=0.75m
Thus, the coordinates of the collision point are:
(4,0.75)
Summary of Results
- Initial velocity V0=8√2m/s
- Time of flight t=0.5s
- Coordinates of collision (4,0.75)
We have two bodies thrown from points A and B. Body A is thrown horizontally from a height of 2 m with a velocity of 8 m/s, and body B is thrown downward at a 45-degree angle from a height of 6 m with an initial velocity V0.
We will set the bottom of tower A (height = 0) as the origin (0, 0). Therefore:
- The height of point A = 2 m (coordinates: (0, 2))
- The height of point B = 6 m (coordinates: (8, 6))
Let t be the time taken for the bodies to collide. The horizontal distance traveled by body A is given by:
xA=8⋅t
xB=V0⋅cos(45∘)⋅t=V0√2⋅t
xA+xB=8
8t+V0√2t=8
Factoring out t:
t(8+V0√2)=8
Thus,
t=88+V0√2
For body A (thrown horizontally):
The vertical position yA after time t is given by:
yA=2−12gt2
Where g=10m/s2.
The vertical position yB after time t is:
yB=6−V0⋅sin(45∘)⋅t−12gt2=6−V0√2t−12gt2
The difference in heights when they collide is:
yB−yA=4
Substituting the equations for yA and yB:
(6−V0√2t−12gt2)−(2−12gt2)=4
This simplifies to:
6−2−V0√2t=4
Thus:
4−V0√2t=4
This leads to:
−V0√2t=0
From the previous equation, we can isolate V0:
V0=8√2
Substituting V0 back into the time equation:
t=88+8√2√2=88+8=816=0.5s
For body A:
xA=8⋅t=8⋅0.5=4m
yA=2−12⋅10⋅(0.5)2=2−12⋅10⋅0.25=2−1.25=0.75m
(4,0.75)
- Initial velocity V0=8√2m/s
- Time of flight t=0.5s
- Coordinates of collision (4,0.75)
Similar Questions
From points A and B, at the respective heights of 2m and 6m, two bodies are thrown simultaneously towards each other, one is thrown horizontally with a velocity of 8m/s and the other, downward at an angle 45∘ to the horizontal at an initial velocity v0 such that the bodies collide in flight. This horizontal distance between points A and B equal to 8m.Then find
a)The initial velocity V0 of the body thrown at an angle 45∘
b)The time of flight t of the bodies before colliding
c) The coordinate (x,y) of the point of collision (consider the bottom of the tower A as origin )is
View SolutionTwo bodies are thrown simultaneously from the same point. One thrown straight up and the other at an angle α with the horizontal. Both the bodies have velocity equal to u. Find the separation between the bodies at time t.
View Solution
Knowledge Check
A body is thrown horizontally with a velocity u from the top of a tower.The displacement of the stone when the horizontal and vertical velocities are equal is
Au2gBu2gC√5(u22g)D2u2gA body is thrown with a velocity of 9.8m/s making an angle of 30∘ with the horizontal. It will hit the ground after a time
A1.5sB1sC3sD2sFrom the top of a tower 20m high, a ball is thrown horizontally. If the line joining the point of projection to the point where it hits the ground makes an angle of 45∘ with the horizontal, then the initial velocity of the ball is:
A10ms−1B4ms−1C15ms−1D3ms−1
Two bodies were thrown simultaneously from the same point, one, straight up, and the other, at an angle of θ=60∘ to the horizontal. The initial velocity of each body is equal to v0=25m/s. Neglecting the air drag, find the distance between the bodies t=1.70s later.
View SolutionTwo bodies were thrown simultaneously from the same point , on straight up and the other, at angle θ=60∘ to the horizontal . The initial velocity of each body is equal to u=30m/s. Neglecting the air resistance, find the distance between the bodies after 2 seconds.
View SolutionTwo bodies were thrown simultaneously from the same point, one straight up, and the other at an angle of θ=30∘ to the horizontal. The initial velocity of each body is 20ms−1. Neglecting air resistance, the distance (in meter) between the bodies at t=1.2 later is
View SolutionA body of mass m is projected with velocity v at an angle of 45∘ with the horizontal. Find the change in its momentum at the end of flight.
View SolutionFrom the the top of a tower 19.6 m high, a ball is thrown horizontally. If the line joining the point of projection to the point where it hits the ground makes an angle of 45∘ with the horizontal, then the initial velocity of the ball is:-
View Solution
