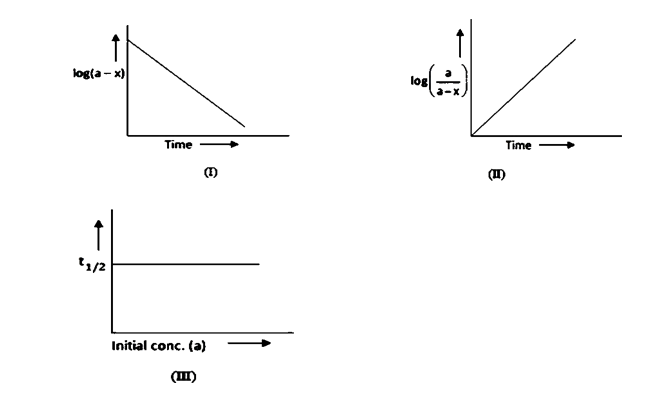
For a first order reaction, if ‘a’ is the initial concentration of reactant, then the half life time is
independent of a
∝a
∝a2
∝a3
The correct Answer is:A
To determine the half-life of a first-order reaction, we can follow these steps:
Step 1: Understand the concept of half-life
The half-life (t₁/₂) of a reaction is the time required for the concentration of a reactant to decrease to half of its initial concentration.
Step 2: Write the integrated rate law for a first-order reaction
For a first-order reaction, the integrated rate law can be expressed as:
ln((A)0(A))=kt
Where:
- (A)0 is the initial concentration of the reactant,
- (A) is the concentration at time t,
- k is the rate constant,
- t is the time.
Step 3: Set up the equation for half-life
At half-life, the concentration of the reactant will be half of the initial concentration:
(A)=(A)02
Substituting this into the integrated rate law gives:
ln⎛⎜⎝(A)0(A)02⎞⎟⎠=kt1/2
Step 4: Simplify the equation
This simplifies to:
ln(2)=kt1/2
Step 5: Solve for half-life
Rearranging the equation to solve for t1/2 gives:
t1/2=ln(2)k
Step 6: Substitute the value of ln(2)
The value of ln(2) is approximately 0.693. Therefore, we can express the half-life as:
t1/2=0.693k
Conclusion
The half-life of a first-order reaction is independent of the initial concentration and is given by the formula:
t1/2=0.693k
The half-life (t₁/₂) of a reaction is the time required for the concentration of a reactant to decrease to half of its initial concentration.
For a first-order reaction, the integrated rate law can be expressed as:
ln((A)0(A))=kt
Where:
- (A)0 is the initial concentration of the reactant,
- (A) is the concentration at time t,
- k is the rate constant,
- t is the time.
At half-life, the concentration of the reactant will be half of the initial concentration:
(A)=(A)02
ln⎛⎜⎝(A)0(A)02⎞⎟⎠=kt1/2
This simplifies to:
ln(2)=kt1/2
Rearranging the equation to solve for t1/2 gives:
t1/2=ln(2)k
The value of ln(2) is approximately 0.693. Therefore, we can express the half-life as:
t1/2=0.693k
The half-life of a first-order reaction is independent of the initial concentration and is given by the formula:
t1/2=0.693k
Similar Questions
Which of the following is/are correct for the first order reaction ? (a is initial concentration of reactant, x is concentration of the reactant reacted and t is time)
View SolutionProve that the half-life period for a first order reaction is quite independent of the initial concentration of reactants.
View Solution
Knowledge Check
If a is the initial concentration of reaction, then the half-life periof of a certain of nth order is
AanBan−1Ca1−nDan+1The half-life of a first order reaction is 30 min and the initial concentration of the reactant is 0.1 M. If the initial concentration of reactant is doubled, then the half-life of the reaction will be
A1800 sB60 minC15 minD900 sThe half life of a first order reaction is 30 min and the initial concentration of the reactant is 0.1 M . If the initial concentration of reactant is doubled ,then the half life of the reaction will be
A1800SB60 minC15 minD900s
In the reaction A→B when the initial concentration of reactant is halved. The half life increases by a factor of eight, what will be order or the reaction?
View SolutionFor the first order reaction half-life time is ………….. on the initial concentration.
View SolutionIn a first order reaction with time the concentration of the reactant decreases
View SolutionHalf life of a first order reaction is 4s and the initial concentration of the reactant is 0.12 M. The concentration of the reactant left after 16 s is
View SolutionIn a zero-order reaction, if the initial concentration of the reactant is doubled, the time required for half the reactant to be consumed
View Solution

