द्रव्यमान M तथा त्रिज्या R वाले एक ठोस गोले में R2 त्रिज्या का एक गोलीय कोटर इस प्रकार स्थित है कि कोटर का केन्द्र गोले के केन्द्र से R/2 दूरी पर है। एक बिन्दु संहति कोटर के अन्दर गोले के केन्द्र से R/4 दूरी पर स्थित है। गोले तथा बिन्दु संहति के मध्य गुरुत्वीय खिंचाव का मान होगा
11GM/R2
14GMm/R2
GM/2R2
GMm/R2
The correct Answer is:B
बिन्दु द्रव्यमान m पर खिंचाव बल की गणना के लिए हम इस पर ठोस गोले से लगने वाले बल की गणना करते हैं तथा इस बल को जो बल खोखले गोले पर लगता है में से घटाते हैं अर्थात्
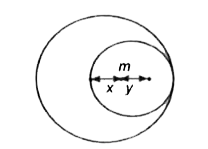
F=GmM(x)2−GmM.y2 [x=R/4,x+y=R/2]
M=(43)πR3ρ and M.=43π(R2)3ρ=M8
F=GMn(R/4)2−Gm(M/8)(R/4)2
=14GmMR2
समान प्रश्न
यदि गोले का सदिश समीकरण, →r2−→r.(8ˆi−6ˆj+10ˆk)−50=0 है, तो गोले के केन्द्र के निर्देशांक और त्रिज्या ज्ञात कीजिए।
View Solutionउस गोले का सदिश समीकरण ज्ञात कीजिए जिसका केन्द्र (2,-3,4) तथा त्रिज्या 5 है।
View Solutionउस गोले का सदिश समीकरण ज्ञात कीजिए जिसका केन्द्र (ˆi+2ˆj−3ˆk) तथा त्रिज्या 5 है।
View Solutionउस गोले का समीकरण ज्ञात कीजिए जो बिंदुओं ( 1,0,0), ( 0,1,0) तथा ( 0,0,1) से होकर जाता है तथा जिसका केंद्र समतल 3x−y+z=2पर स्थित है।
View Solutionयदि गोले का संदिश समीकरण r^(2) - vec( r ) . ( 8vec( i ) - 6 vec( j ) + 10 vec( k )) - 50 = 0 है तो गोले का केंद्र और त्रिज्या ज्ञात कीजिए।
View Solutionउस गोले का समीकरण ज्ञात कीजिए जो बिंदुओं (1,0,0) , ( 0,1,0) तथा ( 0,0,1) से होकर जाता है तथा जिसका केंद्रे समतल x - y + z = 2 पर स्थित है।
View Solutionउस गोले का समीकरण ज्ञात कीजिए जिसका केन्द्र (2, 2, 1 ) तथा त्रिज्या 4 है।
View SolutionA regular pyramid has a square base. The height of the pyramid is 22 cm and side of its base is 14 cm. Volume of pyramid is equal to the volume of a sphere. What is the radius (in cm) of the sphere?
एक सम पिरामिड का आधार एक वर्ग है। पिरामिड को ऊँचाई 22 से.मी. है तथा उसके आधार की भुजा 14 से.मी. है। पिरामिड का आयतन एक गोले के आयतन के बराबर हैं गोले की त्रिज्या (से.मी. में) क्या है?
View Solution
