P and Q are the mid-points of the sides CA and CB respectively of a ΔABC, right angled at C. Prove that 4(AQ2+BP2)=5AB2.Solution in Tamil
Step by step video & image solution for P and Q are the mid-points of the sides CA and CB respectively of a Delta ABC, right angled at C. Prove that 4(AQ^(2)+BP^(2))=5 AB^(2). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
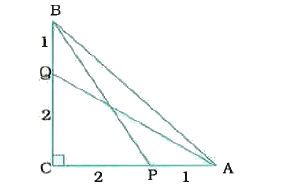
In a right trianlge ABC right angled at C, P and Q are the points on the sides CA and CB respectively which divide these sides in the ratio 2 : 1. Prove that 9(AQ2+BP2)=13AB2.
View Solutionसमकोण त्रिभुज ΔABC में भुजाओं AC तथा CB पर क्रमशः P व Q बिंदु हैं और ∠C समकोण हैं। सिद्ध कीजिए कि AQ2+BP2=AB2+PQ2
View SolutionIf PB and AQ are the medians of a ΔABC right angled at C. Prove that
4(AQ2+BP2)=5AB2
View SolutionP and Q are points on the sides CA and CB of a ΔABC , right angled at C. Prove that AQ2+BP2=AB2+PQ2.
View Solution△ABC -এর ∠C হলো সমকোণ। P এবং Q হলো CA এবং CB বাহুর মধ্যবিন্দুর স্থানাঙ্ক। প্রমাণ করো- 4(AQ2+BP2)=5AB2
View SolutionP and Q are the mid point of the sides CA and CB respectively of a triangle ABC, right angled at C. then, find the value of 4 (AQ2+BP2).
View SolutionP and Q are points on the sides CA and CB respectively of ABC , right angled at C . Prove that AQ2+BP2=AB2+PQ2 .
View Solutionएक △ ABC, C पर समकोणिक है। भुजाओं CA तथा CB पर क्रमश: P तथा Q मध्य बिन्दु हैं। ऐसे त्रिभुज में,
View Solution
