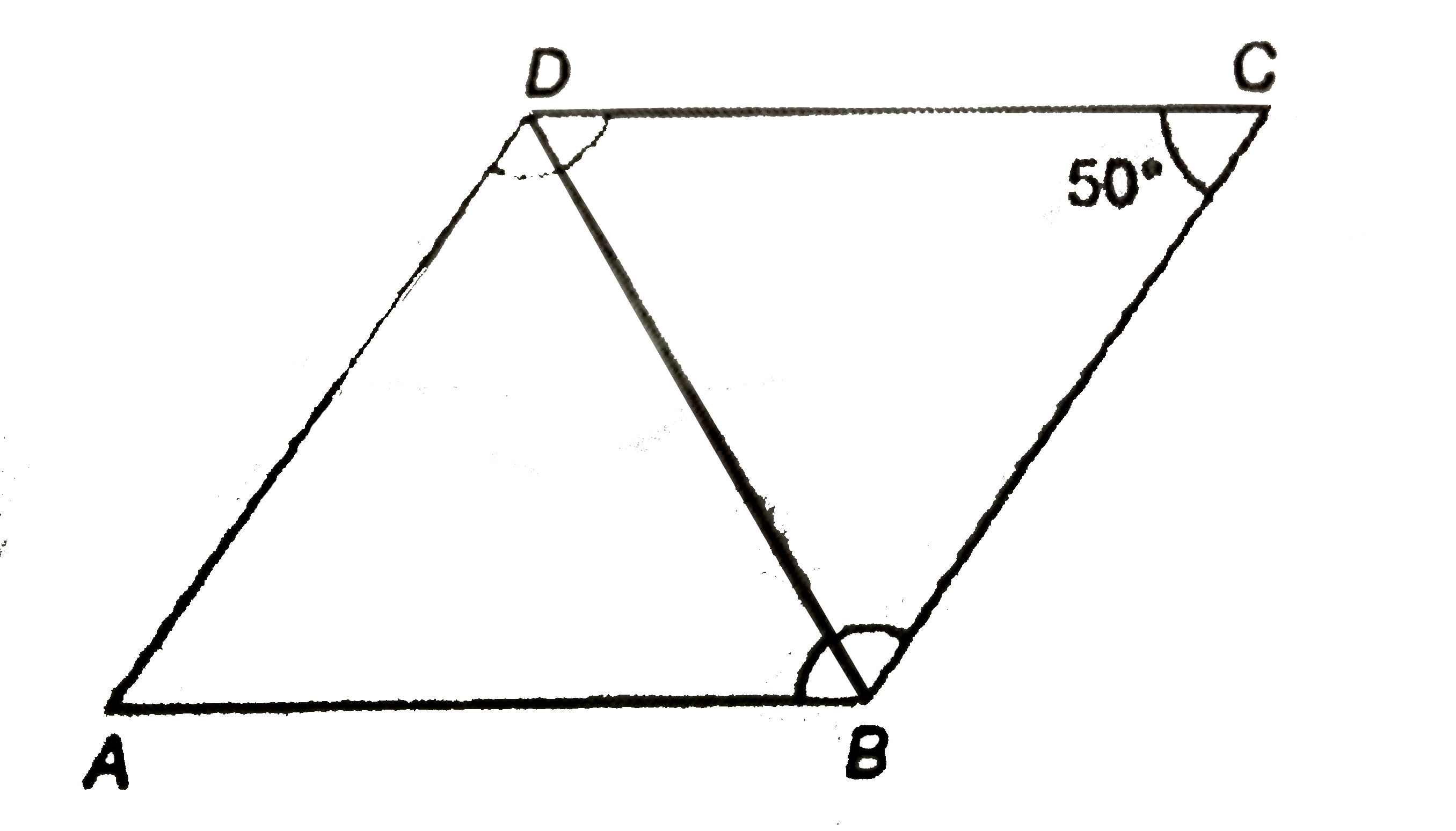
In the figure, ABD, BCD are two triangles. BD is the bisector of ∠ABCand∠ADC.¯¯¯¯¯¯AB || ¯¯¯¯¯¯CDand¯¯¯¯¯¯AD || ¯¯¯¯¯¯BC. If ∠BCD=50∘, then find the angle of ∠BAD.
Video Solution
Text Solution
∠BCD=50∘and¯¯¯¯¯¯BC || ¯¯¯¯¯¯AD.
∠CDA+∠BCD=180∘ (co-interior and angles)
⇒∠CDA+50∘=180∘
∠CDA=180∘−50∘
∠CDA=130∘
Similarly, ∠ABC=130∘ (∵¯¯¯¯¯¯AB || ¯¯¯¯¯¯CD)
Since BD is the bisector of ∠ADCand∠ABC,
∠ABC=∠ABD+∠CBD (∵∠ABD=∠CBD)
2∠ABD=130∘⇒∠ABD=∠CBD=1302=65∘
∠ADB+∠BDC=130∘and∠ADB=∠BDC=1302=65∘
lnΔABD,∠ABD+∠ADB+∠BAD=180∘
130∘+∠BAD=180∘
∠BAD=180∘−130∘=50∘
|
Topper's Solved these Questions
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
48 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - SHORT ANSWER TYPE QUESTIONS
19 Videos
- FRACTIONS AND DECIMALS BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FRACTIONS AND DECIMALS EXERCISE - Crossword
1 Video
- MENUSRATION BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MENUSRATION EXERCISE - Crossword
1 Video
Similar Questions
Knowledge Check
If D is the mid -point of side AB of ΔABC, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯BC+¯¯¯¯¯¯AC=
A2(¯¯¯¯¯¯AD−¯¯¯¯¯¯BD)B2(¯¯¯¯¯¯DC−¯¯¯¯¯¯BD)C2(¯¯¯¯¯¯BD−¯¯¯¯¯¯CA)D2(¯¯¯¯¯¯BD−¯¯¯¯¯¯AC)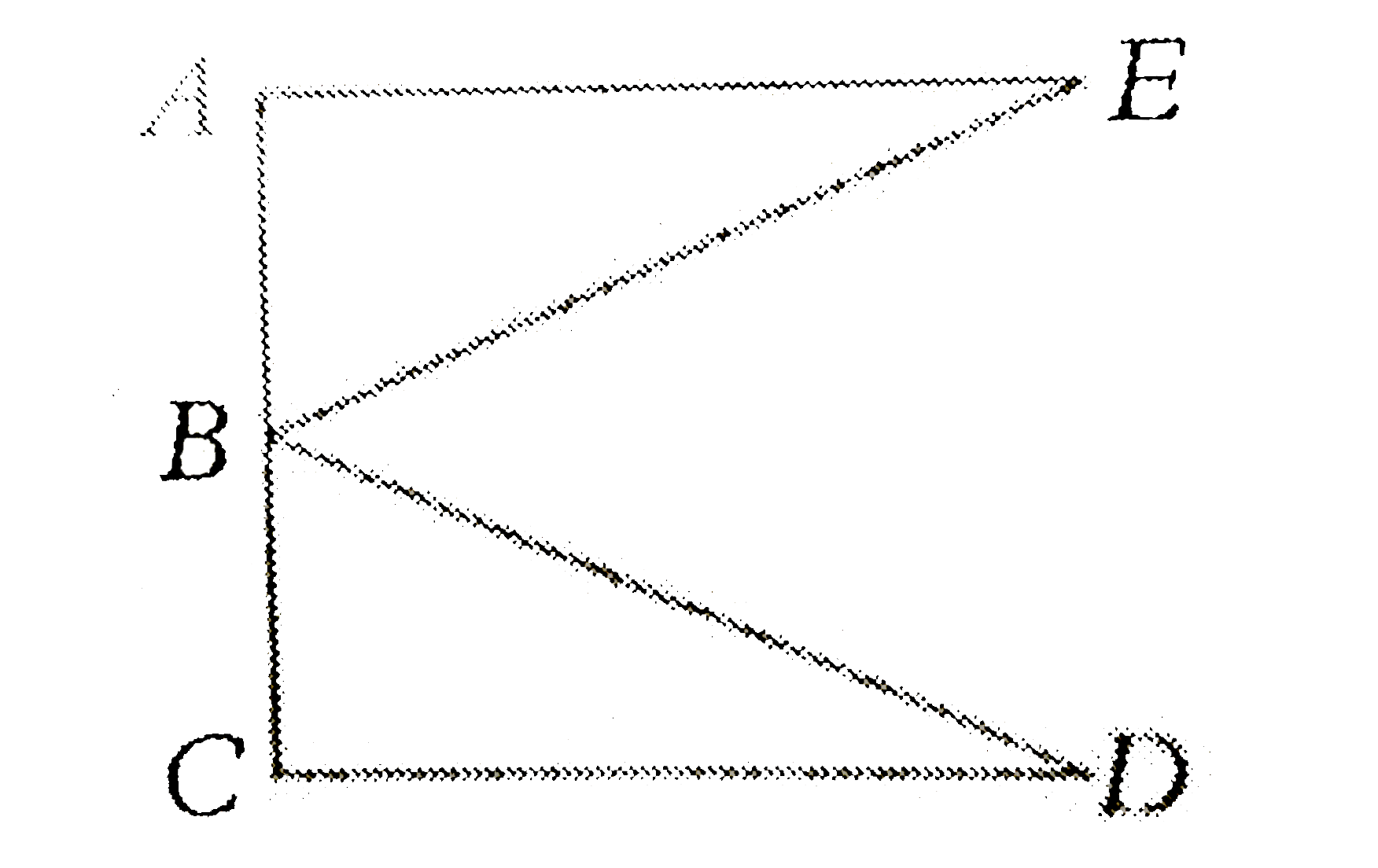
In the given figure, ¯¯¯¯¯¯AE∣∣¯¯¯¯¯¯CD, AB=BC, and AE=CD. If ¯¯¯¯¯¯AC⊥¯¯¯¯¯¯CDand∠AEB=35∘, then find ∠DBE.A70∘B65∘C55∘D50∘If ABCD is a square, then
¯¯¯¯¯¯AB+2¯¯¯¯¯¯BC+3¯¯¯¯¯¯CD+4¯¯¯¯¯¯DA =A4 ¯¯¯¯¯¯ACB3 ¯¯¯¯¯¯ACC2 ¯¯¯¯¯¯CAD¯¯¯¯¯¯AC
In the figure if EC is the bisector of ∠BCDandAB||CD||EF. Find ∠ABC
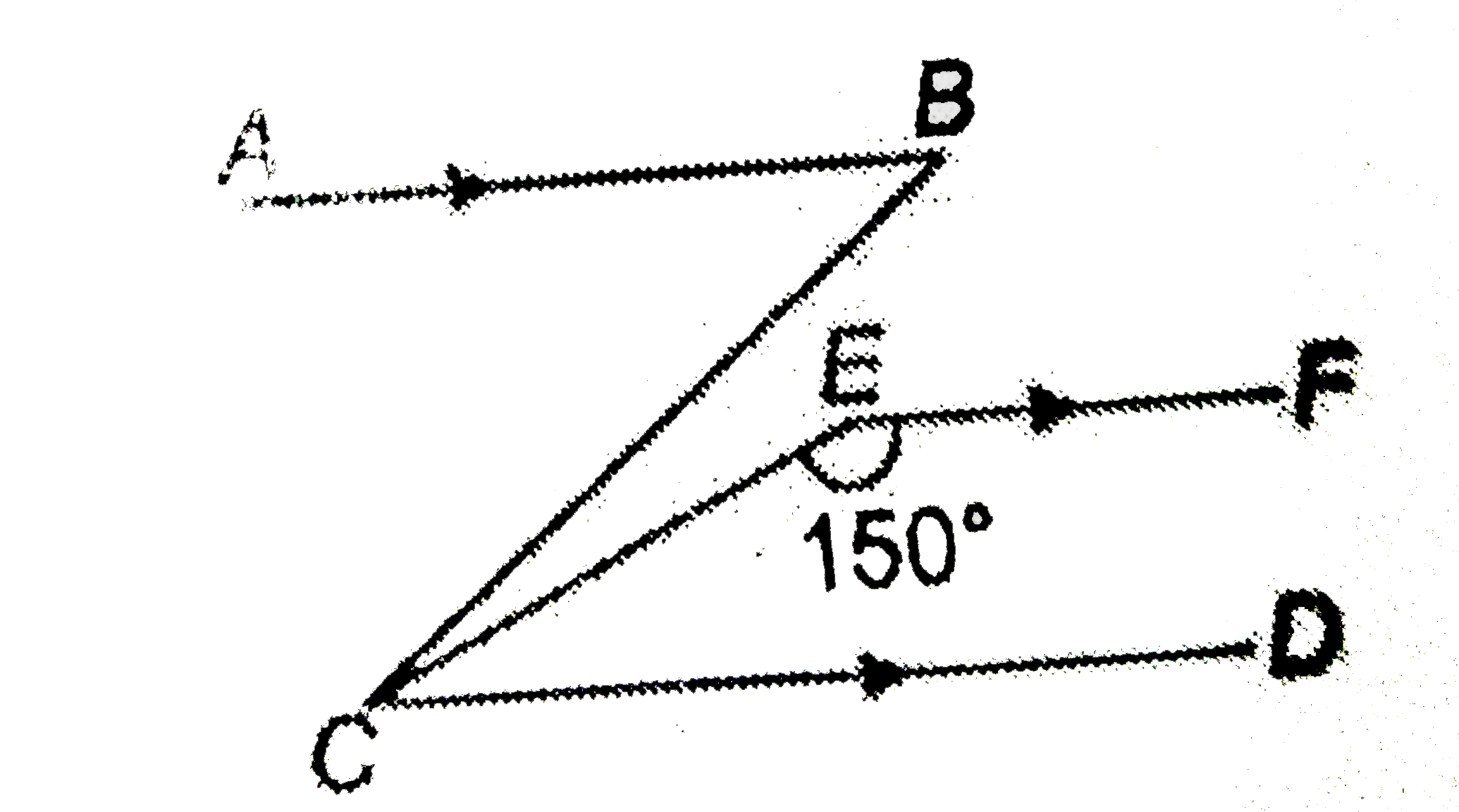
View SolutionIn the following figure (not to scale), ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD. If ∠BAE=25∘ and ∠DCE=30∘, then find ∠AEC.
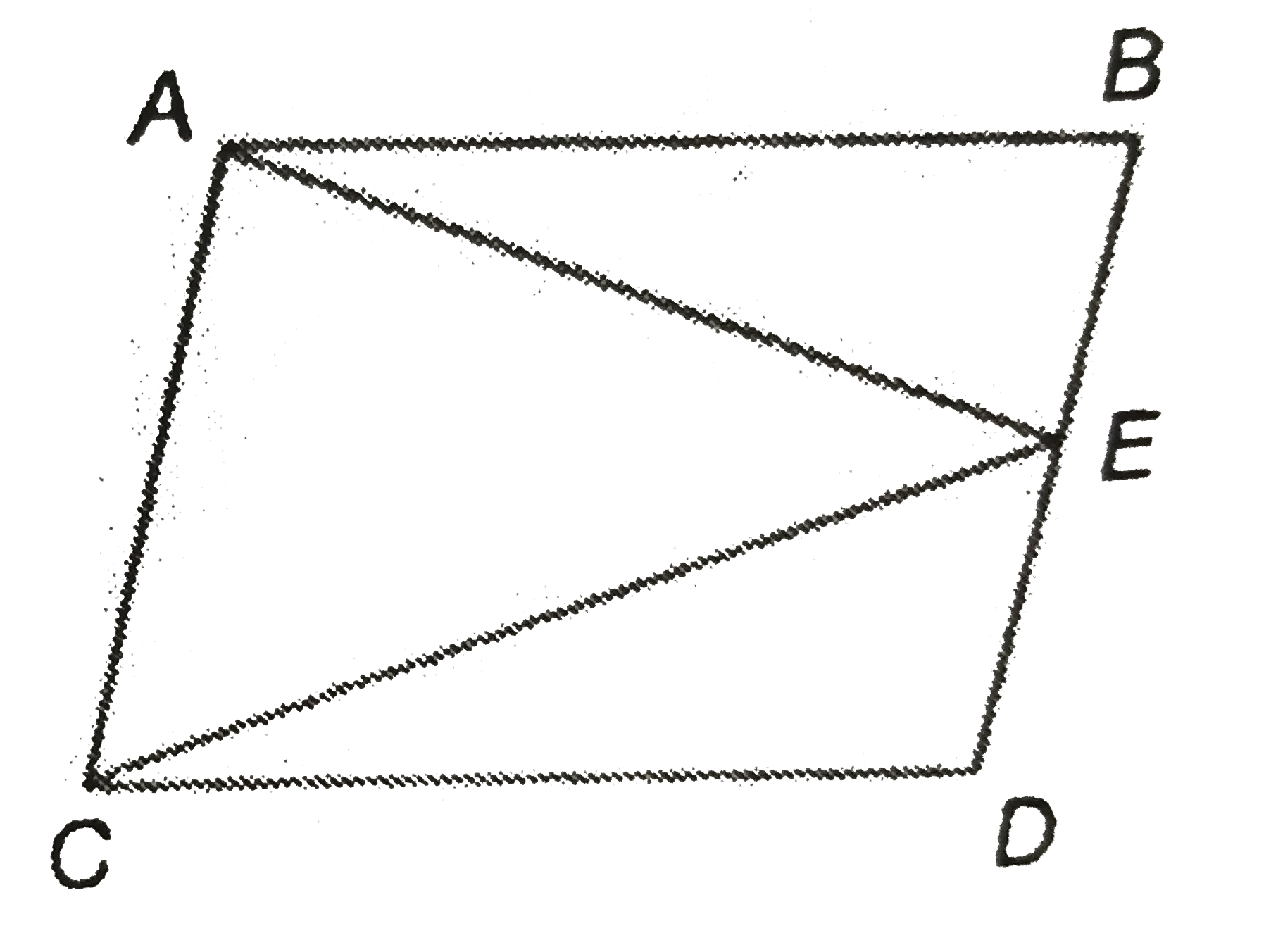
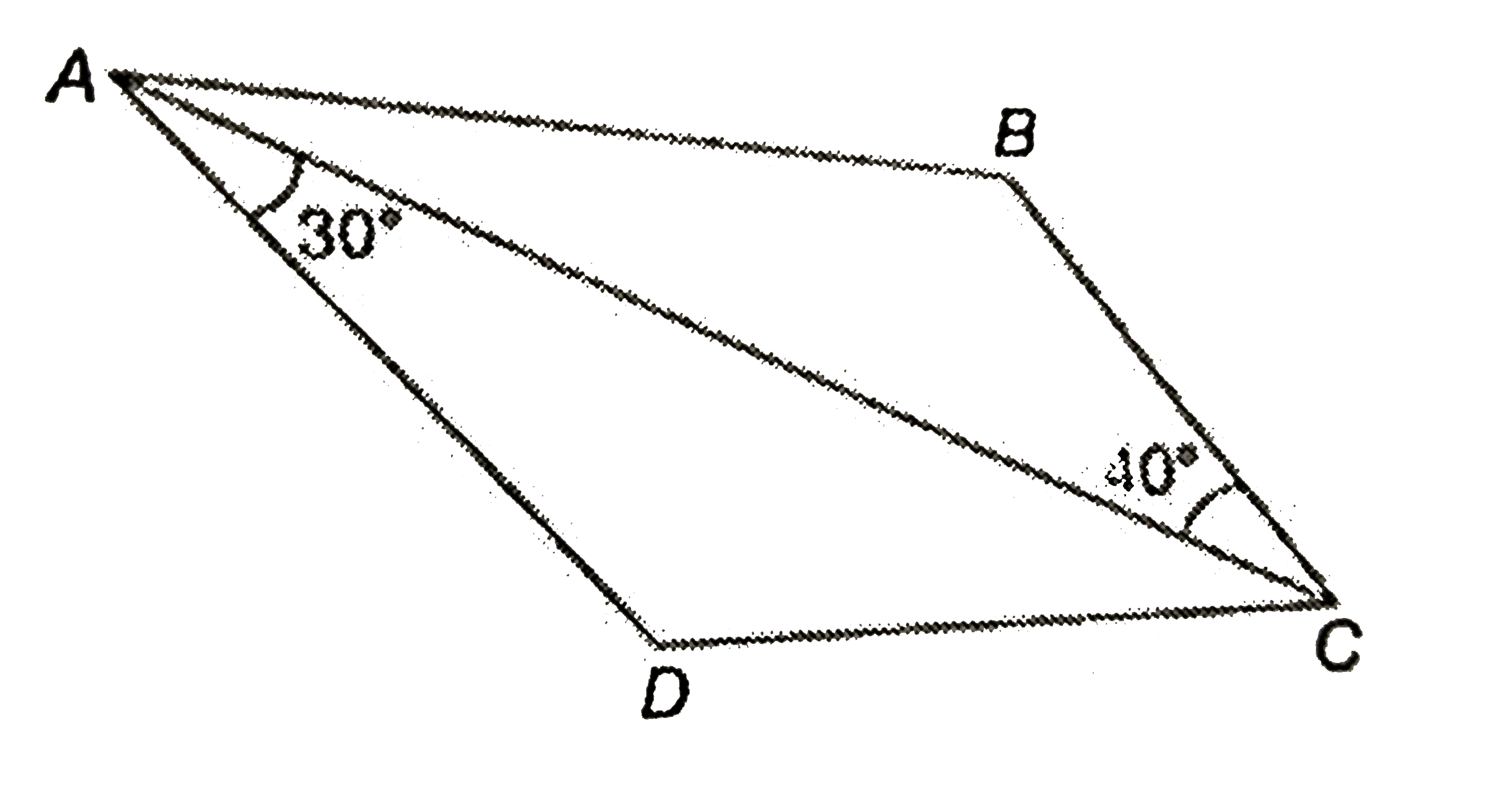
View SolutionIn the figure, ¯¯¯¯¯¯DC || ¯¯¯¯¯¯AB. If ∠ACB=40∘ and ∠CAD=30∘, AC is the bisector of ∠DAB, then find the angle of ∠ADC.
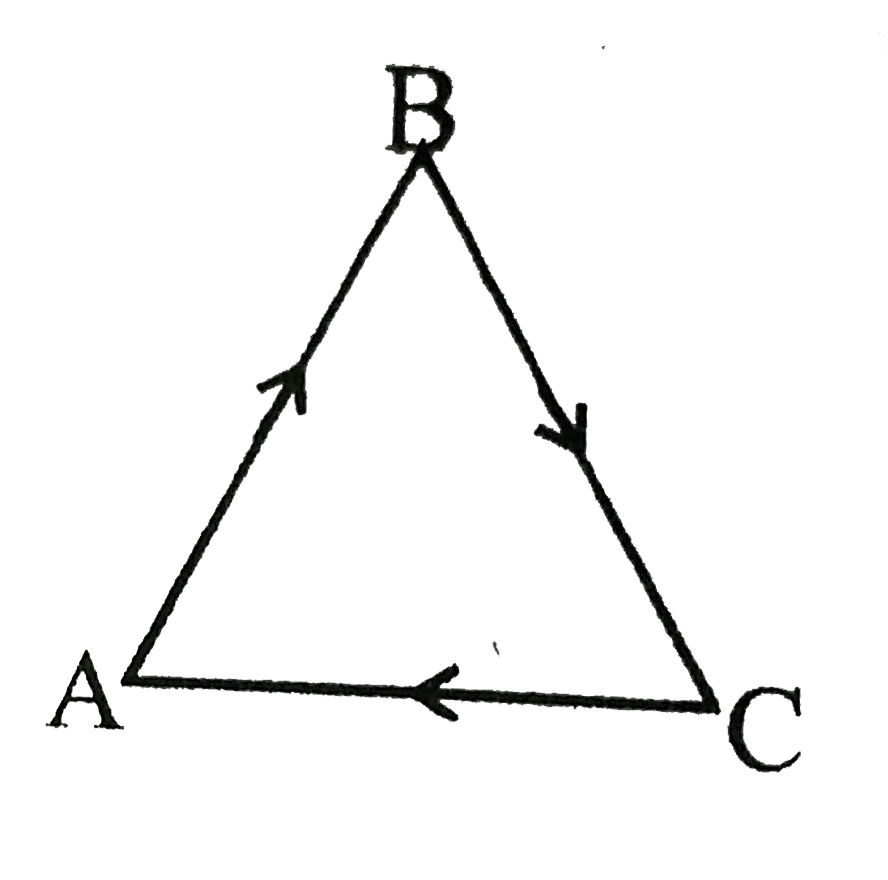
View SolutionWhat is the angle between ?
(i) ¯¯¯¯¯¯ABand¯¯¯¯¯¯AC
(ii) ¯¯¯¯¯¯ABand¯¯¯¯¯¯BC
View Solution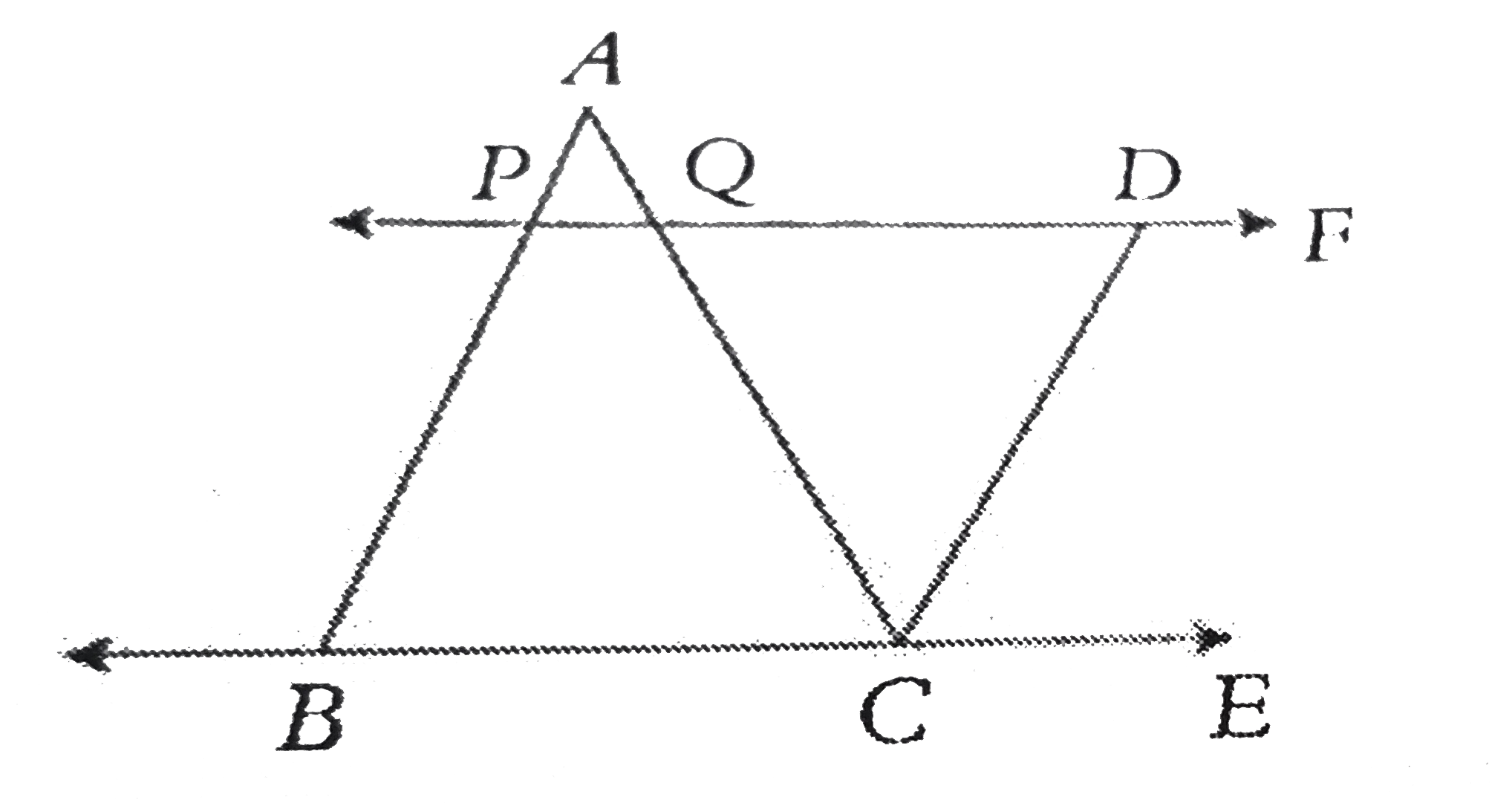 In the figure above ( not to scale), ¯¯¯¯¯¯PF∣∣¯¯¯¯¯¯BE and ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD. If ∠FDC=130∘ and ∠ACD=20∘, find ∠ACB and ∠ABC
In the figure above ( not to scale), ¯¯¯¯¯¯PF∣∣¯¯¯¯¯¯BE and ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD. If ∠FDC=130∘ and ∠ACD=20∘, find ∠ACB and ∠ABC
View Solution

