
In the figure, t intersects two parallel lines p and q. Find the angles of 4x−15∘and3x−15∘.
The correct Answer is:75∘
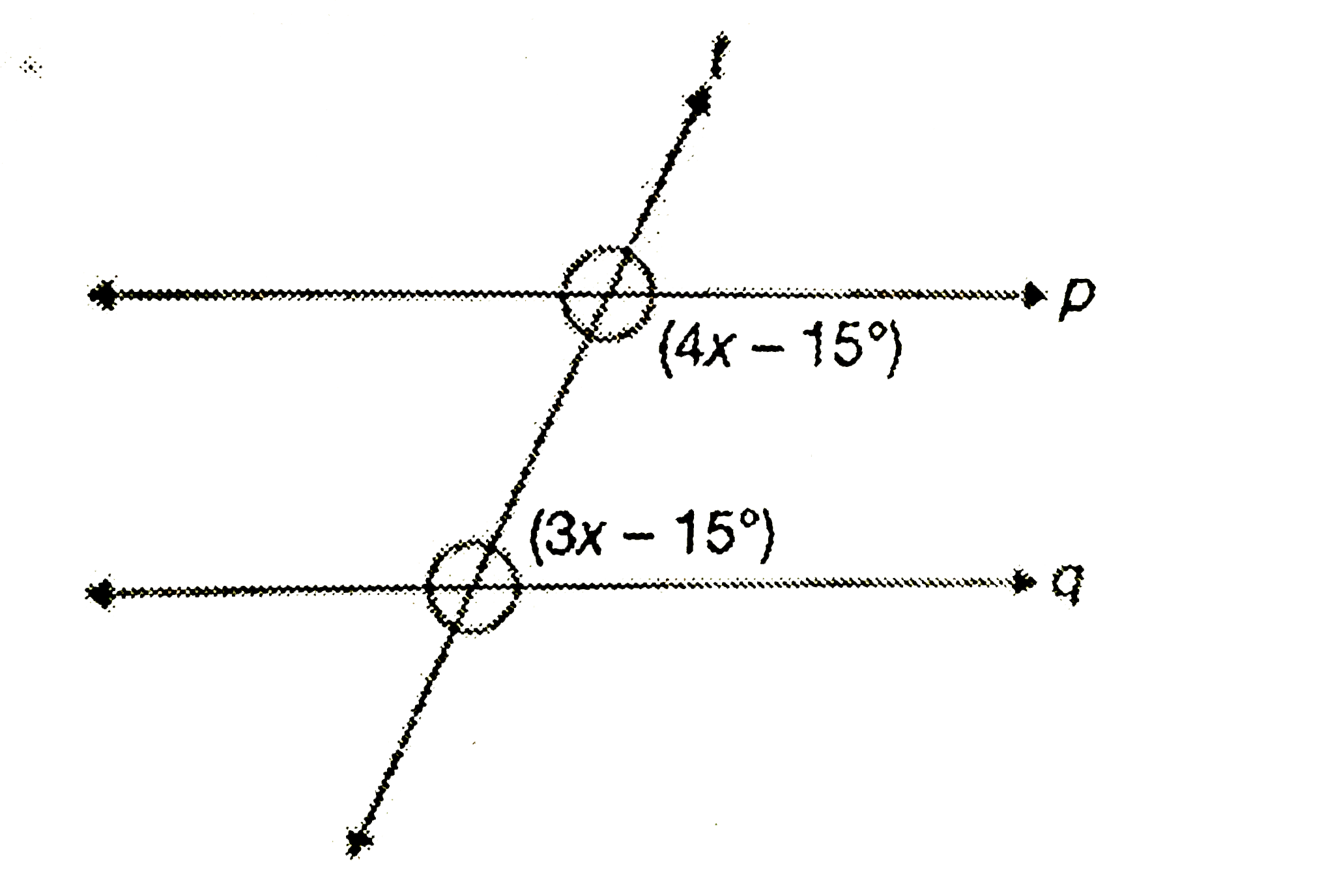
Given p, q and parallel lines and t is a transversal.
Given angles are co-interior angles.
⇒=4x−15∘+3x−15∘=180∘
⇒7x−30∘=180∘
⇒7x=210∘
x=30∘
∴4x−15∘=4×30∘−15∘
=120∘−15∘
=105∘
3x−15∘=3x−15∘
=3×30∘−15
=90−15∘
=75∘
Similar Questions
Knowledge Check
If two interior angles on the same side of a transversal intersecting two parallel lines are in the ratio 3:2, then the greater of the two angles is :
A72∘B36∘C108∘D44∘
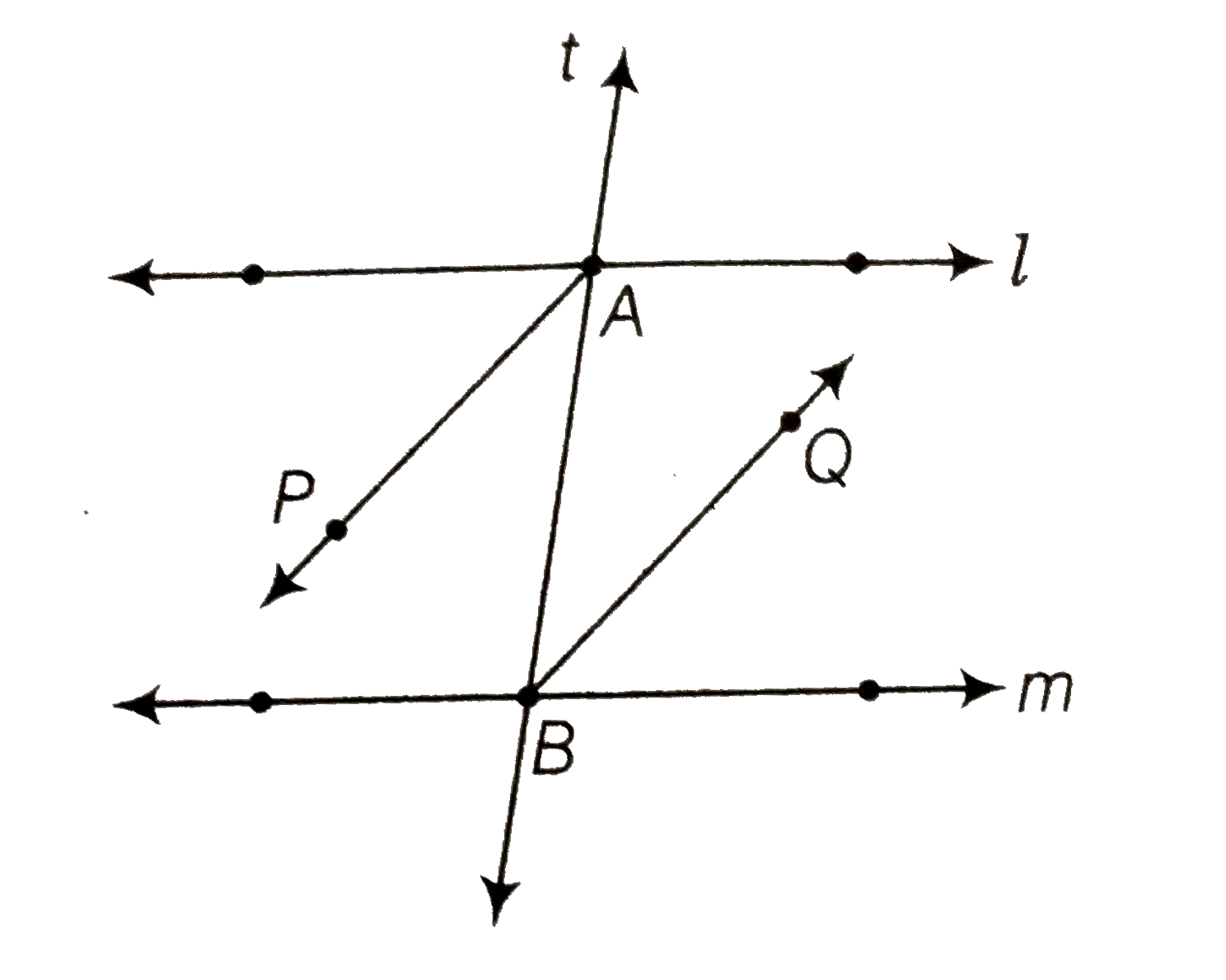
AP and BQ are the bisectors of the two alternate interior angles formed by the intersection of a transversal t with parallel lines l and m (in the given figure). Show that AP||BQ.
View Solutionfind x if 3tan(x−15∘)=tan(x+15∘)
View SolutionIf the direction ratios of two parallel lines are 4, -3, -1 and p + q, 1 + q , 2, then find the values of p and q.
View SolutionThe line through (4,3)and(−6,0) intersects the line 5x+y=0. Find the angles of intersection.
View SolutionIn the adjoining figure, three coplanar lines AB, CD and EF intersect at a point O, forming angles as shown. Find the values of x, y, z and t.

View SolutionThe given figure shows that two parallel lines cut by the transversal AB. If ∠a:∠b=4:5, find the angles a,b,c,d,e and x.
View Solutionl and m are two parallel lines intersected by another pair of parallel lines p and q as shown in figure. Show that ABC≅CDA.

View Solution


