
In the above figure, O is the centre of the circle and AB=CD. If ∠APB=110∘, then find the angle made by the chord CD at the centre.
A
220∘
B
110∘
C
120∘
D
140∘
Video Solution
Text Solution
The correct Answer is:d
(i) Equal chords subtend equal angles at the centre.
(ii) JoinAO, OC, OB and OD.
(iii) Reflex ∠AOB=2∠APB, use this to find ∠AOB as ∠AOB=360∘−2∠APB
(iv)∠AOB=∠COD
|
Similar Questions
Knowledge Check

In the above figure, O is the centre of the circle and AB=CD. If ∠APB=110∘, then find the angle made by the chord CD at the centre.A220∘B110∘C120∘D140∘
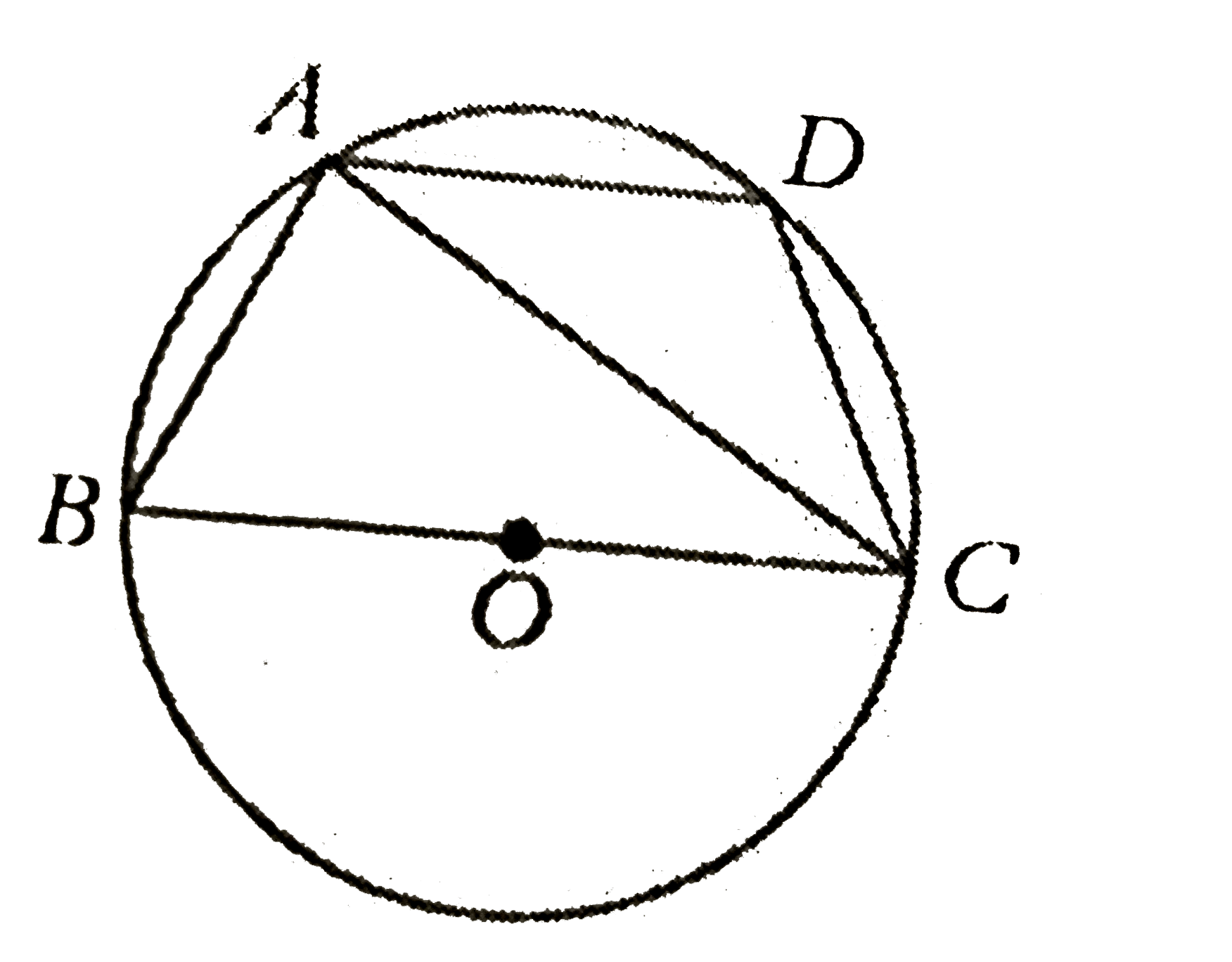
In the above figure, O is the centre of the circle AB,AD and CD are the chords . If ∠ADC=130∘ then fid ∠ACB.
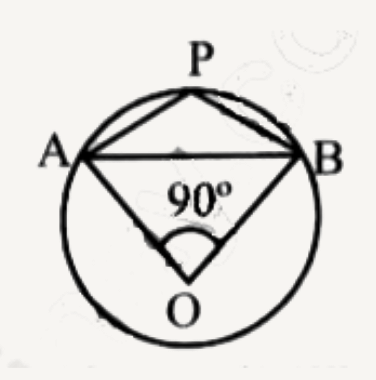
View SolutionIn the given figure, O is the centre of the circle, ∠AOB=90∘. Find ∠APB :
View SolutionIn the adjoining figure, O is the centre of the circle. AB and CD are equal chords.
If ∠AOB=100∘, then find ∠CED.
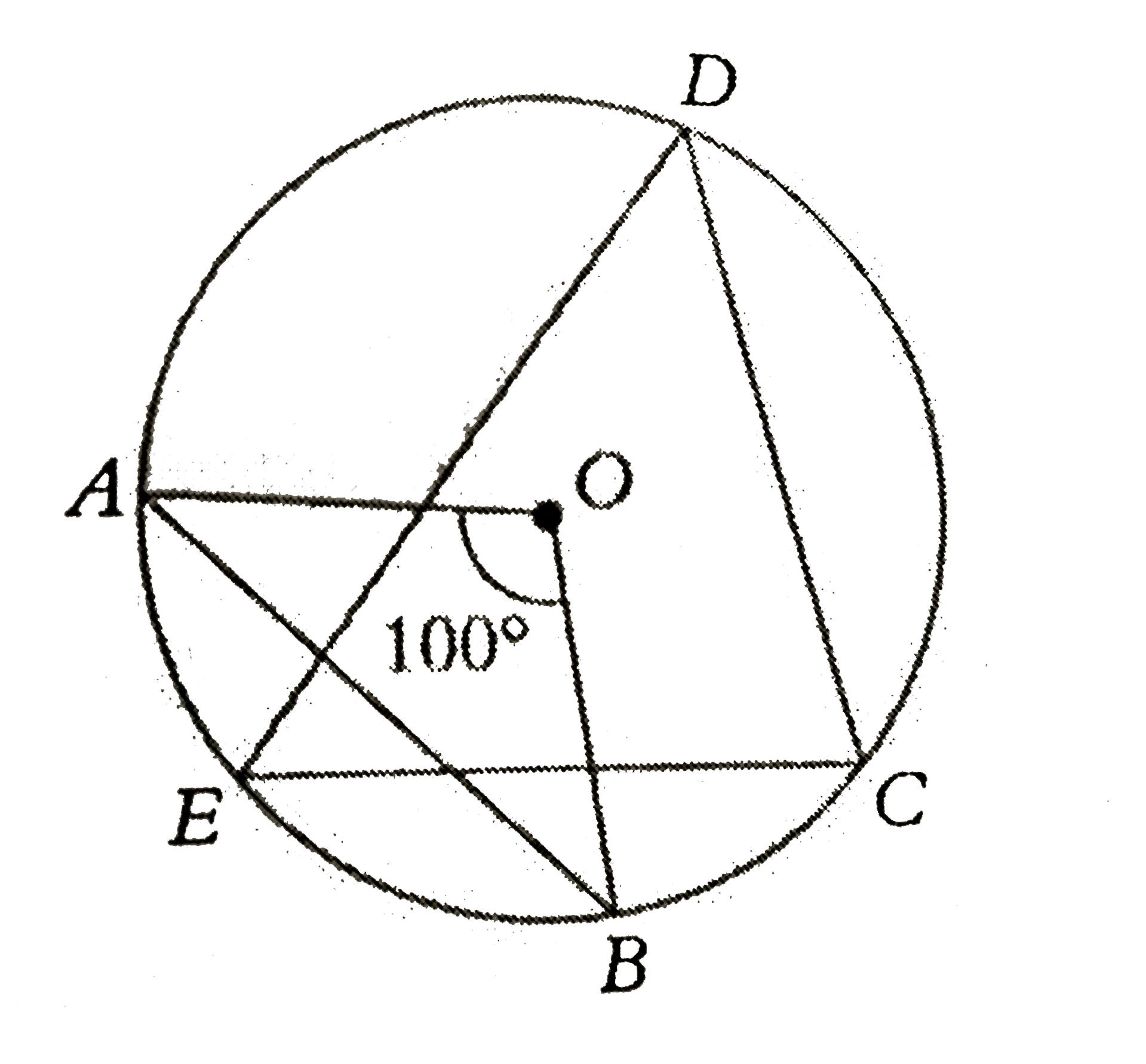
View SolutionIn Figure, O is the centre of the circle. If ∠APB=500, find ∠AOB and ∠OAB
View SolutionIn the following figure, O is the centre of the circle. AB and CD are equal chords. If ∠AOB=100∘ , Find the ∠CED.

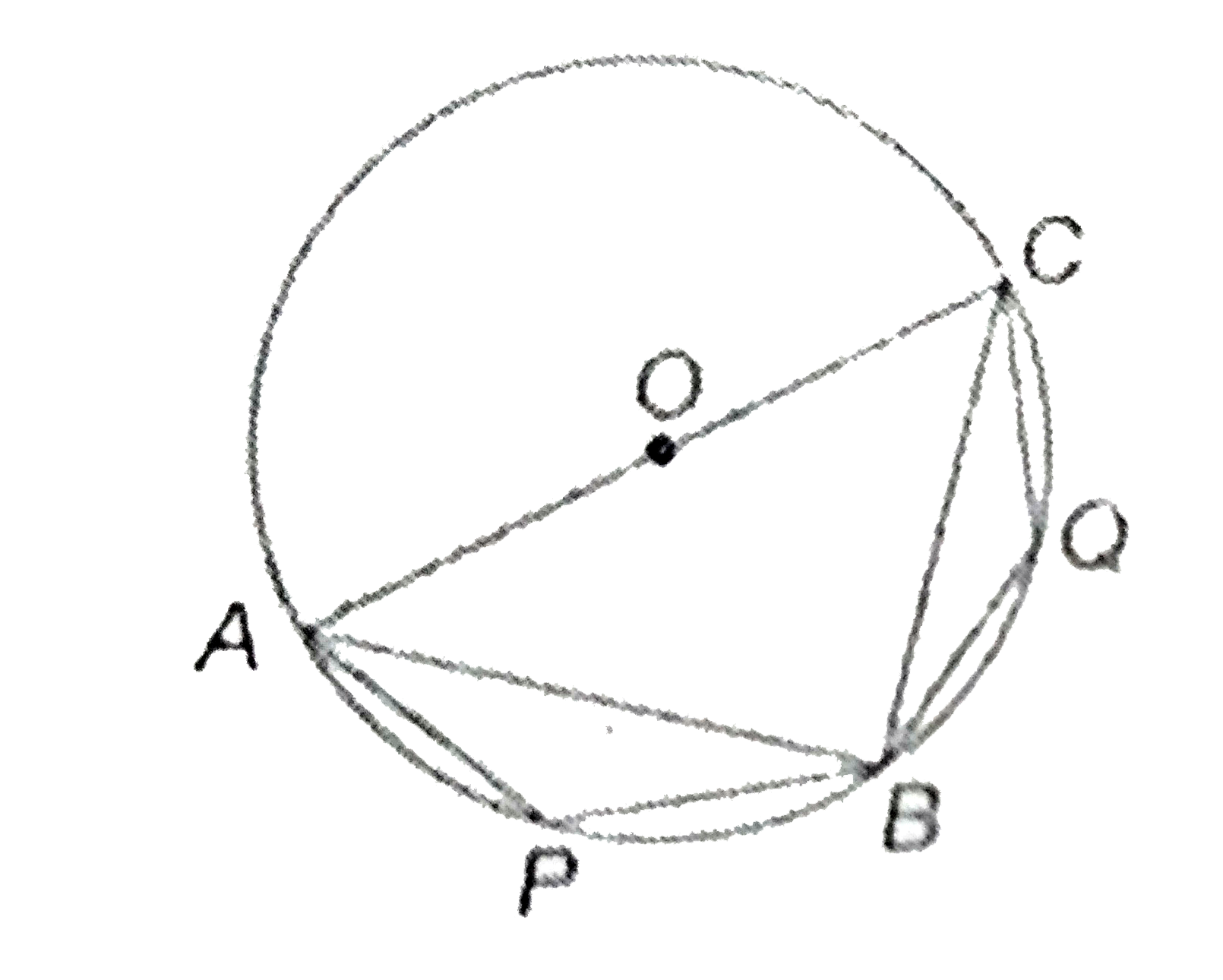
View SolutionIn the following figure, O is the centre of the circle , AC is the diameter and if ∠APB=120∘ , then find ∠BQC .
View SolutionIf figure, O is the centre of the circle, BD=ODandCD⊥AB. Find∠CAB.

View Solution
