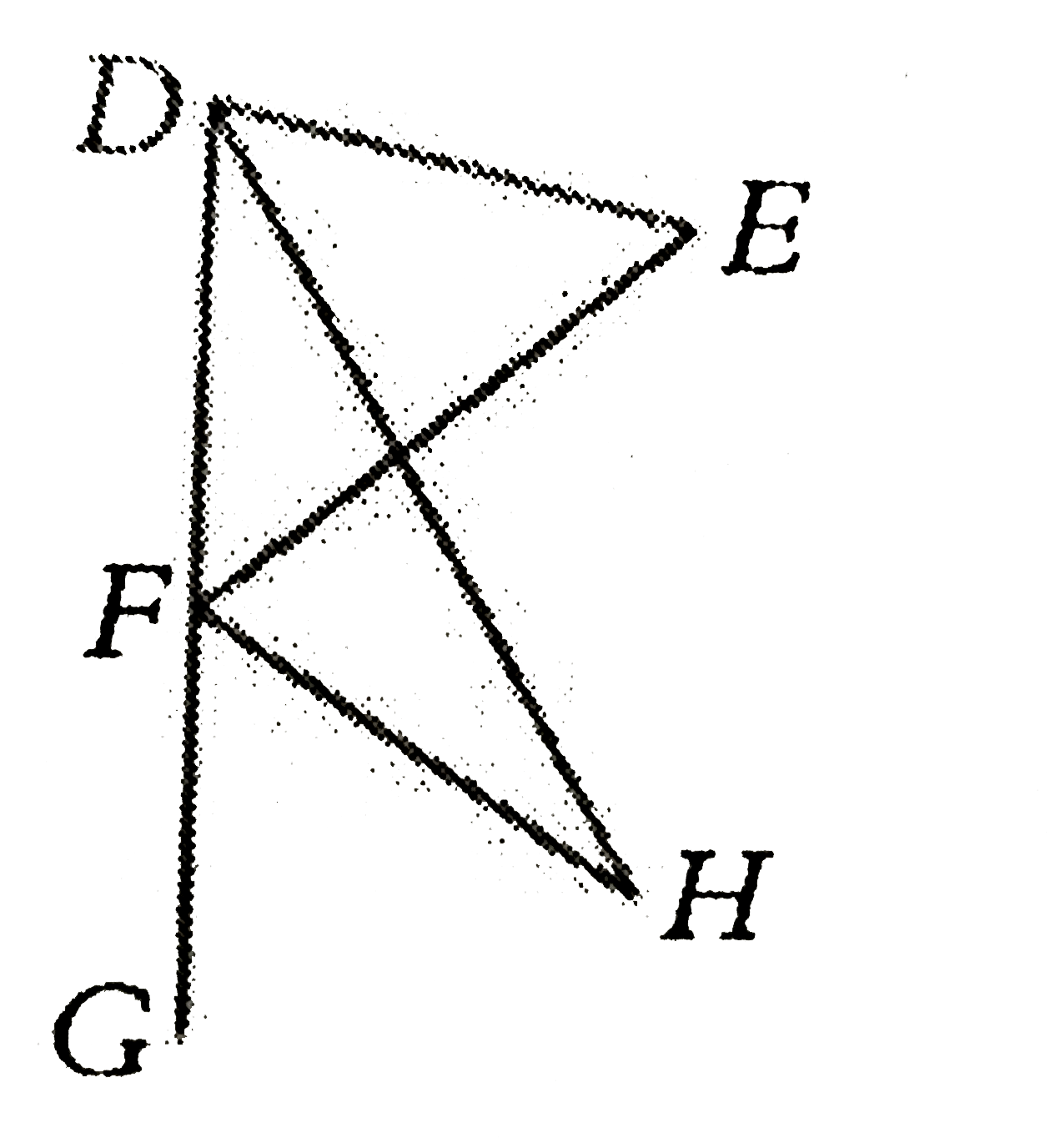
In the abve figure, DEF is a triangle whose side DF is produced to G. HF and HD are the bisectors of ∠EFG and ∠EDG respectively . If ∠DEF=2312.∘ and ∠DHF ( in degrees) =
1112
1125
1134
1113
The correct Answer is:c
(i) DH and FH are angle bisectors. Exterior angle of a triangle equals the sum of its interior opposite anges.
(ii) Take ∠FDH=∠HDE=x and ∠EFH=∠HFG=y.
(iii) ∠EFG is the exterior angle of a ΔDEF.
(iv) ∠DEF=2312.∘ and 2x+y=180∘−2312.∘
(v) Find x and y and H.
∴2y=2x+2312
Simplify to obtain the value of the required angle.
Similar Questions
In the given figure, ΔABC is an equilateral triangle whose side BC has been produced in both the directions to D and E respectively. Prove that ∠ACD=∠ABE.
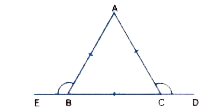
View SolutionThe sides AB and AC of a ΔABC are produced to P and Q respectively. If the bisectors of ∠PBC and ∠QCB meet at O ; Then ∠BOC=90∘−12∠A
View Solution
Knowledge Check

In the above figure , DEF is a triangle whose side DF is produced to G .HF and HD are the bisectors of ∠EFGand∠EDG , respectively . If ∠DEF=231(2)∘ , then ∠DHF (in degrees) = _______.A1112B1125C1134D1113In ΔPQR,PD⊥QR and PO is the bisector of ∠QPR. If ∠PQR=65∘ and ∠PRQ=2312.∘ then ∠DPO in degrees =
A2034B2012C2015D2014In triangle PQR, the sides PQ and PR are produced to A and B respectively. The bisectors of ∠AQRand ∠BRQ intersect at point O. If ∠QOR=50∘, what is the value (in degree) of ∠QPR?
A50B60C80D100
ΔABC~ΔDEF in which AX and DY are the bisectors of ∠Aand∠D respectively . If AX=6.5cmandDY=5.2cm, find the ratio of the areas of ΔABCandΔDEF.
View SolutionIn the given figure, OD and OE are bisectors of ΔCDE and ΔDEB respectively. Find the measures of <1, <2,<3,<4
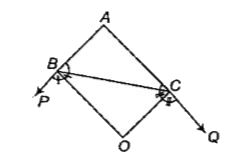
View SolutionIn figure, sides AB and AC of a ΔABC are produced to P and Q, respectively. The bisectors of <PBC and <QCB intersect at O. Tnen. <BOC is equal to
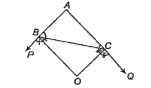
View SolutionIn triangle PQR, the sides PQ and PR are produced to A and B respectively. The bisectors of ∠AQR and ∠BRQ intersect at point O. If ∠QOR=50∘, what is the value (in degree) of ∠QPR?
View SolutionIn figure, sides AB and AC of a ΔABC are produced to P and Q, respectively. The bisectors of ∠PBCand∠QCB intersect at O. Then, ∠BOC is equal to
View Solution
