A coin is biased so that the head is 3 times as likely to occur as tail. If the coin is tossed three times, find the probability distribution of number of tails.
To solve the problem, we need to determine the probability distribution of the number of tails when a biased coin is tossed three times. The coin is biased such that the probability of getting heads (H) is three times that of getting tails (T).
1. Define the Probabilities:
Let P(T) be the probability of getting tails and P(H) be the probability of getting heads. According to the problem, we have:
P(H)=3×P(T)
Since the total probability must equal 1, we can write:
P(H)+P(T)=1
Substituting P(H) in the equation gives:
3P(T)+P(T)=1
4P(T)=1
P(T)=14
Now substituting back to find P(H):
P(H)=3×14=34
2. Determine the Number of Tails:
When the coin is tossed three times, the number of tails (denoted as X) can take values 0, 1, 2, or 3. We will calculate the probability for each of these outcomes.
3. Calculate the Probabilities:
We can use the binomial probability formula:
P(X=k)=(nk)(P(T))k(P(H))n−k
where n=3 (the number of tosses) and k is the number of tails.
- For X=0 (0 tails):
P(X=0)=(30)(14)0(34)3=1⋅1⋅(2764)=2764
- For X=1 (1 tail):
P(X=1)=(31)(14)1(34)2=3⋅14⋅(916)=2764
- For X=2 (2 tails):
P(X=2)=(32)(14)2(34)1=3⋅116⋅34=964
- For X=3 (3 tails):
P(X=3)=(33)(14)3(34)0=1⋅164⋅1=164
4. Probability Distribution Table:
Now we can summarize the probabilities in a table:
| Number of Tails (X) | Probability P(X) |
|----------------------|-------------------------|
| 0 | 2764 |
| 1 | 2764 |
| 2 | 964 |
| 3 | 164 |
Final Probability Distribution:
The probability distribution of the number of tails when the biased coin is tossed three times is as follows:
- P(X=0)=2764
- P(X=1)=2764
- P(X=2)=964
- P(X=3)=164
Let P(T) be the probability of getting tails and P(H) be the probability of getting heads. According to the problem, we have:
P(H)=3×P(T)
Since the total probability must equal 1, we can write:
P(H)+P(T)=1
Substituting P(H) in the equation gives:
3P(T)+P(T)=1
4P(T)=1
P(T)=14
Now substituting back to find P(H):
P(H)=3×14=34
When the coin is tossed three times, the number of tails (denoted as X) can take values 0, 1, 2, or 3. We will calculate the probability for each of these outcomes.
We can use the binomial probability formula:
P(X=k)=(nk)(P(T))k(P(H))n−k
where n=3 (the number of tosses) and k is the number of tails.
P(X=0)=(30)(14)0(34)3=1⋅1⋅(2764)=2764
P(X=1)=(31)(14)1(34)2=3⋅14⋅(916)=2764
P(X=2)=(32)(14)2(34)1=3⋅116⋅34=964
P(X=3)=(33)(14)3(34)0=1⋅164⋅1=164
Now we can summarize the probabilities in a table:
|----------------------|-------------------------|
| 0 | 2764 |
| 1 | 2764 |
| 2 | 964 |
| 3 | 164 |
The probability distribution of the number of tails when the biased coin is tossed three times is as follows:
- P(X=0)=2764
- P(X=1)=2764
- P(X=2)=964
- P(X=3)=164
Similar Questions
A coin is biased so that the head is 3 times as likely to occur as tail. If the coin is tossed twice, find the probability distribution of number of tails.
View SolutionA coin is biased so that a head is twice as likely to occur as a tail. If the coin is tossed 3 times, what is the probability of getting 2 tails and 1 head?
View Solution
Knowledge Check
Three coins are tossed. Then the probability distribution of number of head is
A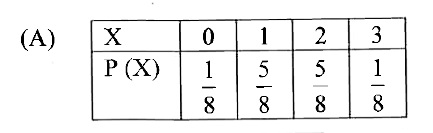 B
B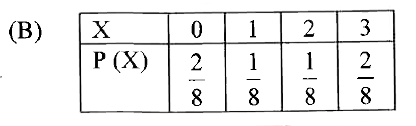 C
C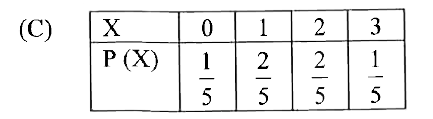 D
D
A coin is tossed three times.What is the probability of getting no tail ?
A12B38C58D18A coin is tossed 5 times. The probability that tail appears an odd number of times, is:
AA. 12BB. 13CC. 25DD. 15
A coin is biased so that heads is three times as likely to appear as tails. Find P(H) and P(T). If such a coin is tossed twice find the probability that head occurs atleast once
View SolutionA coin is biased so that heads is three times as likely to appear as tails. Find P(H) and P(T). If such a coin is tossed twice find the probability that head occurs atleast once
View SolutionA coin is weighted so that head is twice as likely ||to appear as tail. When such a coin is tossed once the probability of getting tail is
View SolutionA coin is tossed 4 times. Find the mean and variance of the probability distribution of the number of tails.
View SolutionA fair coin is tossed three times . The probability that there is atleast one tail is
View Solution
