The members of a consulting firm rent cars from three rental agencies :
50% from agency X, 30% from agency Y and 20% from agency Z. From past experience, it is known that 9% of the cars from agency X need a service and tunning before renting, 12% of the cars from agency Y need a service and tunning before renting and 10% of the cars from agency Z need a service and tunning before renting. If the renting car delivered to the firm neeeds service and tunning, find the probability that agency Z is not to be blamed.
The correct Answer is:81101.
To solve the problem, we will use Bayes' theorem and the law of total probability. We need to find the probability that a car needing service is not from agency Z.
Step 1: Define the events
Let:
- AX: the event that the car is from agency X
- AY: the event that the car is from agency Y
- AZ: the event that the car is from agency Z
- B: the event that the car needs service
Step 2: Determine the probabilities
From the problem statement, we have:
- P(AX)=0.5
- P(AY)=0.3
- P(AZ)=0.2
The probabilities that a car from each agency needs service are:
- P(B|AX)=0.09
- P(B|AY)=0.12
- P(B|AZ)=0.10
Step 3: Calculate the total probability of needing service
Using the law of total probability, we can find P(B):
P(B)=P(B|AX)P(AX)+P(B|AY)P(AY)+P(B|AZ)P(AZ)
Substituting the values:
P(B)=(0.09)(0.5)+(0.12)(0.3)+(0.10)(0.2)
Calculating each term:
P(B)=0.045+0.036+0.02=0.101
Step 4: Calculate the probability that the car is from agency Z given that it needs service
Using Bayes' theorem:
P(AZ|B)=P(B|AZ)P(AZ)P(B)
Substituting the values:
P(AZ|B)=(0.10)(0.2)0.101=0.020.101
Calculating this gives:
P(AZ|B)≈0.198
Step 5: Find the probability that the car is not from agency Z given that it needs service
We need to find P(AcZ|B):
P(AcZ|B)=1−P(AZ|B)
Substituting the value we found:
P(AcZ|B)=1−0.198≈0.802
Final Answer
Thus, the probability that agency Z is not to be blamed when a rented car needs service is approximately 0.802 or 81101.
---
Let:
- AX: the event that the car is from agency X
- AY: the event that the car is from agency Y
- AZ: the event that the car is from agency Z
- B: the event that the car needs service
From the problem statement, we have:
- P(AX)=0.5
- P(AY)=0.3
- P(AZ)=0.2
- P(B|AX)=0.09
- P(B|AY)=0.12
- P(B|AZ)=0.10
Using the law of total probability, we can find P(B):
P(B)=P(B|AX)P(AX)+P(B|AY)P(AY)+P(B|AZ)P(AZ)
Substituting the values:
P(B)=(0.09)(0.5)+(0.12)(0.3)+(0.10)(0.2)
Calculating each term:
P(B)=0.045+0.036+0.02=0.101
Using Bayes' theorem:
P(AZ|B)=P(B|AZ)P(AZ)P(B)
Substituting the values:
P(AZ|B)=(0.10)(0.2)0.101=0.020.101
Calculating this gives:
P(AZ|B)≈0.198
We need to find P(AcZ|B):
P(AcZ|B)=1−P(AZ|B)
Substituting the value we found:
P(AcZ|B)=1−0.198≈0.802
Thus, the probability that agency Z is not to be blamed when a rented car needs service is approximately 0.802 or 81101.
Similar Questions
A car agency has 108 cars. He sold some cars at 9% profit and rest at 36% profit. Thus he gains 17% on the sale of all his cars. The no. of cars sold at 36% profit is :
View SolutionDiscuss the national and international agencies where from secondary data may be collected.
View SolutionA medical company has factories at two places, A and B from these places, supply is made to each of its three agencies situated at P, Q and R. The monthly requirements of the agencies are respectively 40, 40 and 50 packets of the medicines, while the production capacity of the factories, A and B are 60 and 70 packets respectively. The transportation cost per packet from the factories to the agencies are given below.
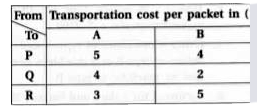
How many packets from each factory be transported to each agency so that the cost of transportation is minimum ? Also find the minimum cost ?
View SolutionA car agency has 108 cars. He sold some cars at 9%profit and rest at 36% profit. Thus he gains 17%on the sale of all his cars. The no. of cars sold at36% profit is:
View SolutionThe members of a consulting firm rent cars from three agencies: 50% from agency X, 30% from agency Y and rest from agency Z. From past experience it is known that 9% of the cars from agency X need a service and tuning before renting, 12% of the cars from agency Y need a service and tuning before renting and 10% of the cars from agency Z need a service and tuning before renting. If the rental car delivered to the firm needs service and tuning, find the probability that agency Z is not to be blamed.
View SolutionThe Government agency responsible for purchasing grains from the farmers, safe storage and distribution
View Solutionसरकार की कौन ऐजेन्सी किसान से खाद्यान्न क्रय करती है?
View SolutionWhich one of the following agencies given below is not the rating agency of an economy?
View Solution

