Select the correct options
Dimensionally correct equation must be correct
Dimensionally correct equation may be incorrect
Dimensionally correct equation may be correct
Dimensionally incorrect equation must be incorrect
The correct Answer is:B, C, D
To solve the question regarding the correctness of the given options based on dimensional analysis, we will analyze each statement step by step.
1. Understanding Dimensional Analysis:
- Dimensional analysis is a method used to check the consistency of equations in physics by comparing the dimensions of the quantities involved.
2. Evaluating the First Option:
- The first option states that "Dimensionally correct equations must be correct."
- This is not necessarily true. While dimensionally correct equations can be valid, they can also be misleading. For example, the equation Torque+Work is dimensionally correct since both have the same dimensions (energy). However, they represent different physical quantities and cannot be added together.
- Conclusion: This option is incorrect.
3. Evaluating the Second Option:
- The second option states that "Dimensionally correct equations may be correct."
- This is true. An equation can be dimensionally correct but still not represent a valid physical relationship. For example, adding energies (work and potential energy) is dimensionally correct and physically valid.
- Conclusion: This option is correct.
4. Evaluating the Third Option:
- The third option states that "Dimensionally incorrect equations must be incorrect."
- This is true. If an equation is dimensionally incorrect, it cannot be a valid physical equation. For example, adding acceleration (dimensions of L/T2) and velocity (dimensions of L/T) is dimensionally incorrect and thus invalid.
- Conclusion: This option is correct.
5. Evaluating the Fourth Option:
- The fourth option states that "Dimensionally incorrect equations must be incorrect."
- This is the same as the third option and is true for the same reasons. If the dimensions do not match, the equation cannot hold true.
- Conclusion: This option is correct.
Final Answer:
Based on the evaluations:
- The correct options are: 2nd, 3rd, and 4th.
- Dimensional analysis is a method used to check the consistency of equations in physics by comparing the dimensions of the quantities involved.
- The first option states that "Dimensionally correct equations must be correct."
- This is not necessarily true. While dimensionally correct equations can be valid, they can also be misleading. For example, the equation Torque+Work is dimensionally correct since both have the same dimensions (energy). However, they represent different physical quantities and cannot be added together.
- Conclusion: This option is incorrect.
- The second option states that "Dimensionally correct equations may be correct."
- This is true. An equation can be dimensionally correct but still not represent a valid physical relationship. For example, adding energies (work and potential energy) is dimensionally correct and physically valid.
- Conclusion: This option is correct.
- The third option states that "Dimensionally incorrect equations must be incorrect."
- This is true. If an equation is dimensionally incorrect, it cannot be a valid physical equation. For example, adding acceleration (dimensions of L/T2) and velocity (dimensions of L/T) is dimensionally incorrect and thus invalid.
- Conclusion: This option is correct.
- The fourth option states that "Dimensionally incorrect equations must be incorrect."
- This is the same as the third option and is true for the same reasons. If the dimensions do not match, the equation cannot hold true.
- Conclusion: This option is correct.
Based on the evaluations:
- The correct options are: 2nd, 3rd, and 4th.
Similar Questions

Select the correct option(s).
View SolutionSelect the correct option.
View Solution
Select the correct option ?

View SolutionSelect the correct option :

View SolutionSelect the correct option
View SolutionSelect the correct options
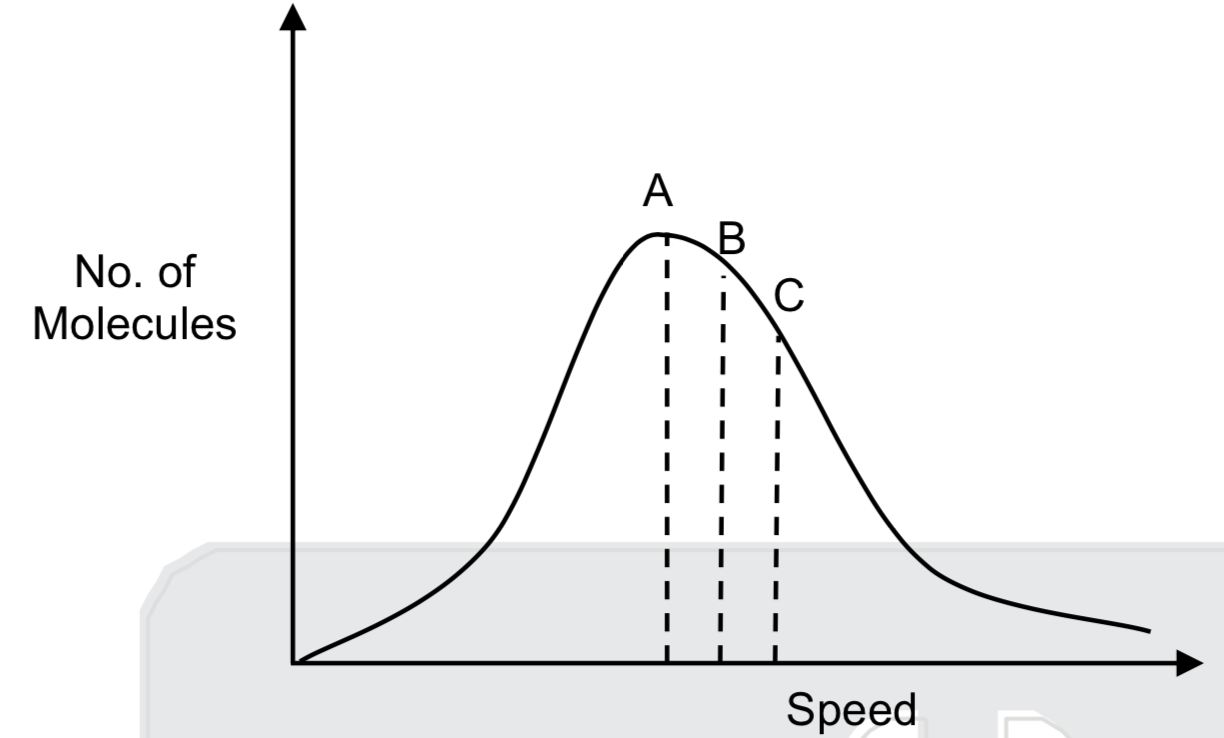 :
:
View SolutionSelect the option with the correct pairing

View SolutionSelect the correct option in the following.
View Solution

