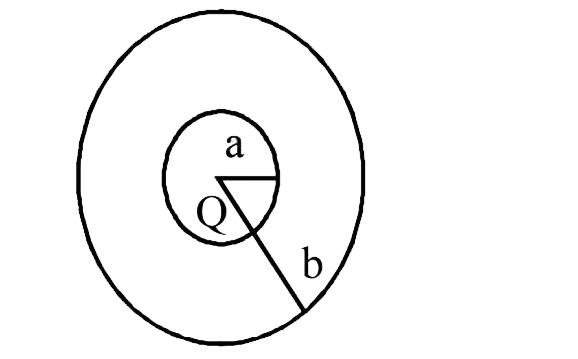
The region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density ρ=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:
Q2πa2
Q2π(b2−a2)
2Qπ(a2−b2)
2Qπa2
The correct Answer is:A
Given volumetric charge density

ρ(r)=Ar
To find the charge enclosed in the region of a < x < b
qin=∫x=rx=aρ(x)dV
qin=∫raAx4πx2dx
qin=4πA[r2−a22]
Now apply Gasses law at point P
∮→E.−→dS=qinε0=1ε0 [Charge at centre + Volumetric charge]
E.4πr2=1ε0[Q+4πA(r2−a22)]
E=Q4πε0r2+A2ε0[1−a2r2]
for electric field to remain constant, we can write following :
Q4πε0r2=A2ε0(a2r2)
A=Q2πa2
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (BC.MCQ))
10 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (C.MCQ))
19 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (BA.MCQ))
3 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
Similar Questions
Let E1(r), E2(r) and E3(r) be the respectively electric field at a distance r from a point charge Q, an infinitely long wire with constant linear charge density λ, and an infinite plane with uniform surface charge density σ. If E1(r0)=E2(r0)=E3(r0) at a given distance r0, then
View SolutionA dipole of Dipole moment →p=p0√2(ˆi+ˆj). Is placed at origin. Now a uniform external electrical filed at magnitude E0 is applied along direction of dipole. Two points A and B are lying on a equipotential surface of radius R centered at origin. A is along axial position of dipole and B is along equatorial position. There correct option are :
_PHY_E01_006_Q01.png)
View SolutionTwo identical charged spheres suspended form a common point by two massless strings of lengths l, are initially at a distance d(d>>l) apart because of their mutual repulsion. The charges brgin to leak from both the spheres at a constant rate. As a result, the spheres approach each other with a velocity v. Then v varies as a function of the distance x between the spheres, as
View SolutionDefine the term 'stopping potential' in relation to photoelectric effect.
View SolutionWill any emf be induced between the ends of a vertical magnetic pole falling through the plane of magnetic meridian?
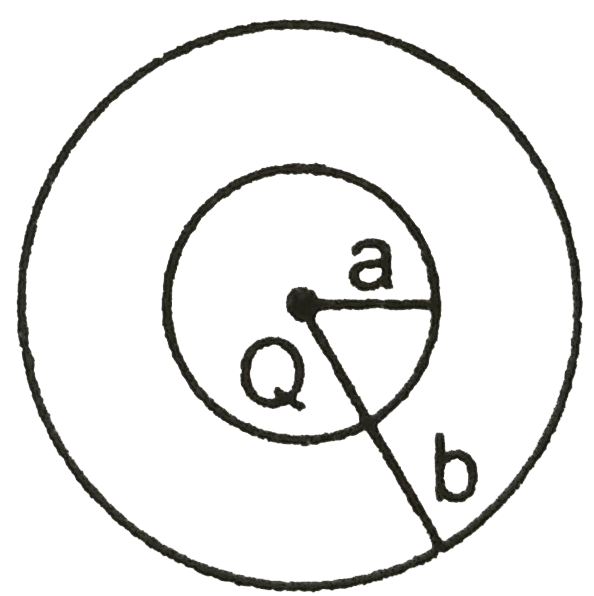
View SolutionThe region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density rho=A/r , where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:
View Solutionत्रिज्या a तथा b के दो संकेन्द्री गोले के बीच के स्थान में आयतन आवेश घनत्व ρ=A/r है जहाँ A स्थिरांक है तथा r केंद्र से दूरी है गोले के केंद्र पर एक बिंदु आवेश Q है A का वह मान बताये जिससे गोले के बीच के स्थान में एकसमान विधुत क्षेत्र हो
View SolutionA system consits of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density rho=alpha/r , where alpha is a positive constant and r is the distance from the centre of the sphere. Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R.
View SolutionAn insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
View SolutionAn insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
View SolutionCharge density of a sphere of radius R is rho = rho_0/r where r is distance from centre of sphere.Total charge of sphere will be
View SolutionThe region between two concentric spheres of radii 'a' and 'b', respectively (see figure), has volume charge density rho =A/r , where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant is :
View SolutionThe region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density ρ=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:

View SolutionCharge density of a sphere of radius R is rho = rho_0/r where r is distance from centre of sphere.Total charge of sphere will be
View SolutionA system consits of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density ρ=αr, where α is a positive constant and r is the distance from the centre of the sphere. Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R.
View SolutionA system consists of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density rho=alpha/r , where alpha is a positive constant and r is the distance from the centre of the sphere. Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R.
View Solution

