In an AC circuit of 100 Hz, the effective value of current is 6 A. Calculate (i) the peak value of current (ii) mean value of current over half cycle and (iii) value of current 1/ 500 s after it was zero .
To solve the problem step by step, we will break it down into three parts as per the question.
Given Data:
- Frequency (f) = 100 Hz
- Effective (RMS) value of current (I_rms) = 6 A
Part (i): Calculate the peak value of current (I_0)
1. Formula for Peak Current: The relationship between the RMS current and the peak current is given by:
I0=√2×Irms
2. Substituting the values:
I0=√2×6A
3. Calculating:
I0=1.414×6=8.485A≈8.48A
Answer for Part (i):
The peak value of current (I_0) is 8.48 A.
---
Part (ii): Calculate the mean value of current over half cycle
1. Formula for Mean Current: The average current over half a cycle is given by:
Iavg=2I0π
2. Substituting the peak current:
Iavg=2×8.48π
3. Calculating:
Iavg=16.963.14159≈5.4A
Answer for Part (ii):
The mean value of current over half cycle is 5.4 A.
---
Part (iii): Calculate the value of current 1/500 s after it was zero
1. Current Equation: The instantaneous current in an AC circuit is given by:
I(t)=I0sin(ωt)
where ω=2πf.
2. Calculate ω:
ω=2π×100=200πrad/s
3. Substituting time: We need to find the current at t=1500s:
I(1500)=I0sin(200π×1500)
4. Calculating the argument of sine:
200π×1500=200π500=2π5
5. Substituting back into the current equation:
I(1500)=8.48sin(2π5)
6. Calculating sin(2π5):
sin(2π5)≈0.9511
7. Final calculation:
I(1500)≈8.48×0.9511≈8.065A
Answer for Part (iii):
The value of current 1/500 s after it was zero is approximately 8.065 A.
---
- Frequency (f) = 100 Hz
- Effective (RMS) value of current (I_rms) = 6 A
I0=√2×Irms
I0=√2×6A
I0=1.414×6=8.485A≈8.48A
The peak value of current (I_0) is 8.48 A.
Iavg=2I0π
Iavg=2×8.48π
Iavg=16.963.14159≈5.4A
The mean value of current over half cycle is 5.4 A.
I(t)=I0sin(ωt)
where ω=2πf.
ω=2π×100=200πrad/s
I(1500)=I0sin(200π×1500)
200π×1500=200π500=2π5
I(1500)=8.48sin(2π5)
sin(2π5)≈0.9511
I(1500)≈8.48×0.9511≈8.065A
The value of current 1/500 s after it was zero is approximately 8.065 A.
Similar Questions
If the effective value of current in 50 Hz a.c. circuit is 5.0 A, What is (i) peak value or current (ii) mean value of current over half a cycle (iii) value of current 1/300 s after it was zero ?
View SolutionIf the peak value of a current in 50Hz AC. Cirucit is 7.07 A. What is the mean value of current over half a cycle and the value of current 1/300s after it was zero?
View Solution
Knowledge Check
if the effective value of A.C in a circuit is 10A, then the peak value of current a
Aa. 10ABb. 1√2ACc. 14.14ADd. 5AThe rms value of current in an ac circuit is 25 A, then peak current is
A35.36mAB35.36AC3.536AD49.38AIn the circuit shown in the figure
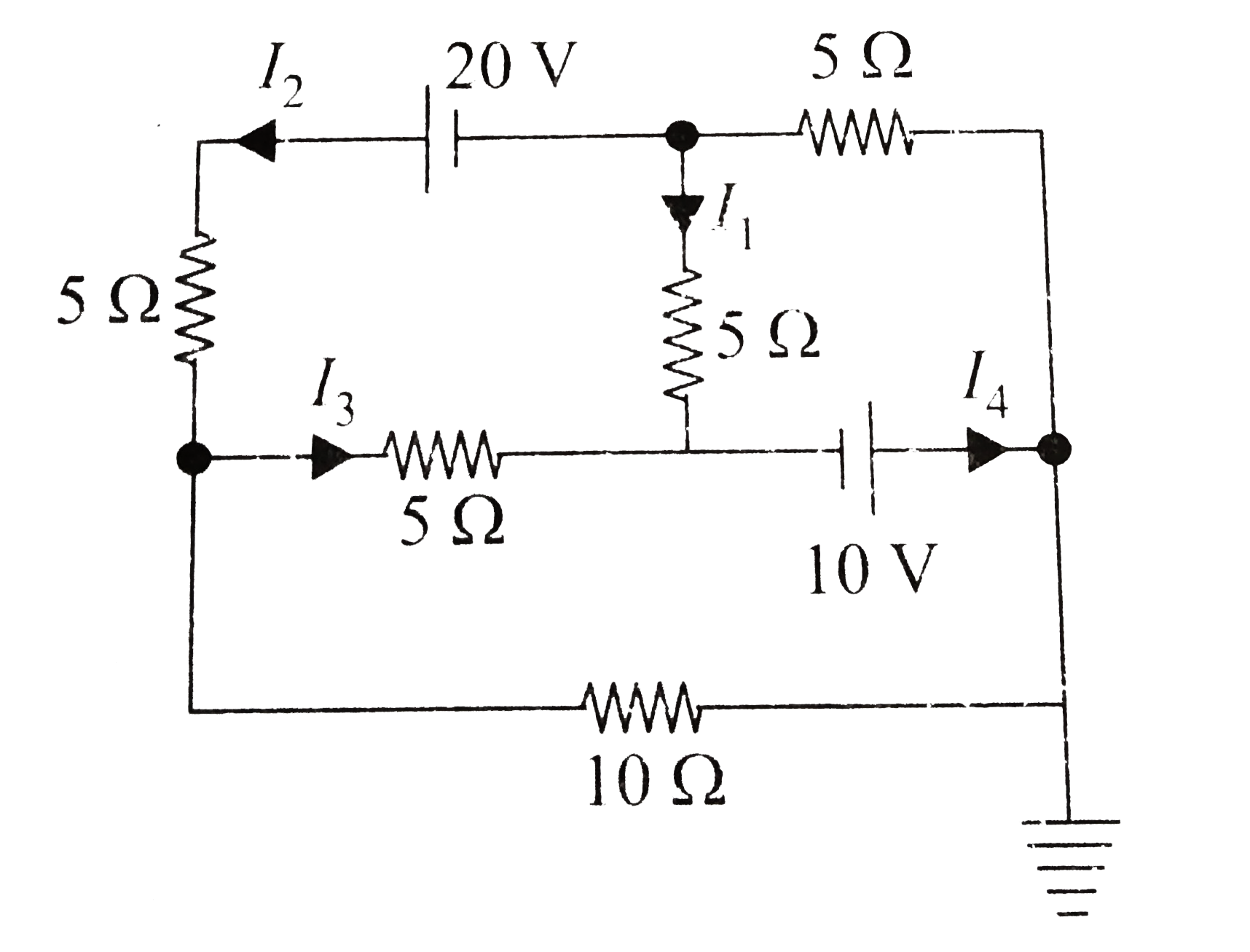 .
.
The value of current I1 isA2ABzeroC2.5 ADnone of these
Find the peak value and mean value of current over a half cycle if effective current in 40 Hz AC circuit is 7 A .
View SolutionThe effective value of current in a 50 cycle a.c. circuit is 5 A. what is the value of current 1/300 second after it was zero?
View SolutionThe effective value of current in a 50 cycle a.c. circuit is 5.0 A. What is the value of current (1/300) s after it is zero ?
View SolutionThe equation of a.c.in a circuit is I=50sin100πt. Find (i) frequency of a.c.
(ii) mean value of a.c over positive half cycle
(iii) value of current 1300s after it was zero.
View SolutionThe mean value of current for half cycle for a current variation shown by the graph is
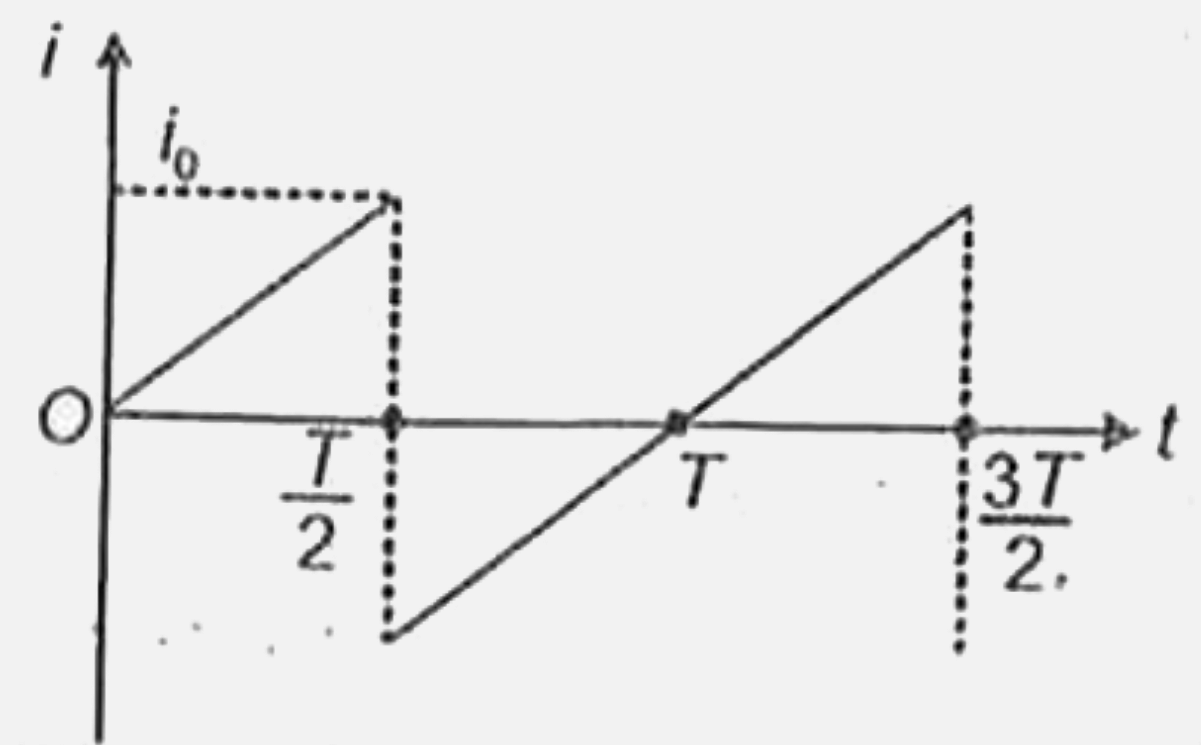
View Solution
