If A(3,4) and B(−5,−2) are the extremities of the base of an isosceles triangle ABC with tan C=2, then point C can be
A
(3√5−12,−(1+2√5))
B
⎛⎜ ⎜⎝−(3√5+5)2,3+2√5⎞⎟ ⎟⎠
C
(3√5−12,3−2√5)
D
⎛⎜ ⎜⎝−(3√5−5)2,−(1−2√5)⎞⎟ ⎟⎠
Text Solution
The correct Answer is:A, B
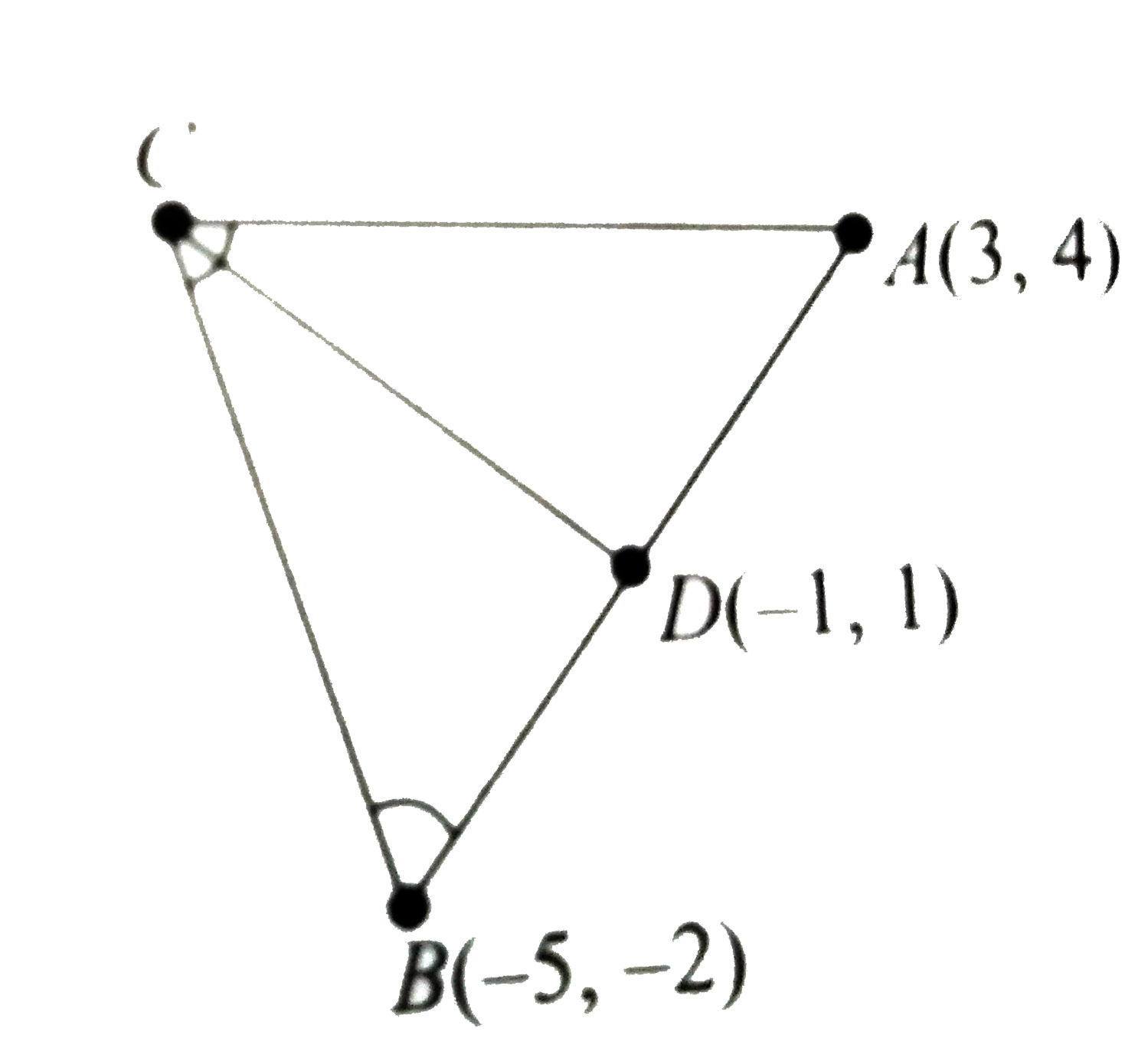
D(−1,1) is midpoint of AB.
CD=BDcot.C2=5.cot.C2
Now, tanC=2
⇒2tan.C21−tan−2.C2=2
⇒tan2.C2+tan.C2−1=0
⇒tan.C2=−1+√52
⇒cot.C2=√5+12
⇒CD=5(√5+12)=52(√5+1)
Slope of BD is 3/4.
∴ Slope of CD is −4/3=tanα
Using parametric form of straight line, coordinates of C are given by
⎛⎜
⎜⎝−1±5(√5+1)2cosα,1±5(√5+1)2sinα⎞⎟
⎟⎠
or (−5+3√52,2√5+3) and (3√5−12,−(2√5+1))
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If A(3, 5, -4), B(-1, 1, 2) and C(-5, -5, -2) are the vertices of Δ ABC, then the triangle is
AscalaneBright angledCequilateralDisoscelesIf in a triangle ABC, b + c = 3a, then tan(B2)tan(C2) is equal to
A1/2B1/3C1/4D1/5If in a triangle ABC,S=a2−(b−c)2 then tan A is equal to
A12B817C815D1516
The extremities of the base of an isosceles triangle ΔABC are the points A(2.0) and B(0,1). If the equation of the side AC is x=2 then the slope of the side BC
View SolutionIf A(-2,1),B(2,3) and C(-2,-4) be the vertices of a △ABC, show that tanB=23
View SolutionNumber of non-similar isosceles triangles ABC such that tan A + tan B + tan C = 300 is equal to
View SolutionProve that there exist exactly two non-similar isosceles triangles ABC such that tanA+tanB+tanC=100.
View SolutionShow that the points A(7, 10), B(-2, 5) and C(3, -4) are the vertices of an isosceles right-angled triangle.
View Solution

