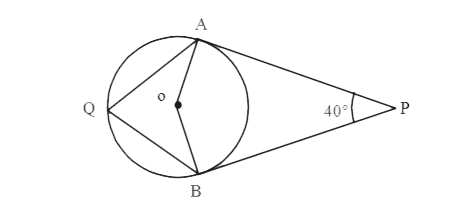
In the given, figure , O is the centre of the circle and AD is a tangent to the circle at.A if ∠CAD=55∘ and ∠ADC=25∘, then find ∠ABO.

Video Solution
Text Solution
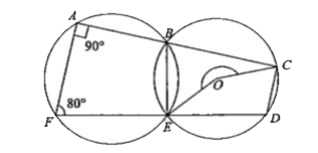
(i) Join OA and OC.
(ii) ∠ACD=180∘−80∘=100∘.
(iii) ∠ACBand∠ACD are supplementary.
⇒∠ACB+∠ACD=180∘.
⇒∠ACB=80∘
(iv) ∠AOB=2∠ACB.⇒AOB=2×80∘=160∘
(v) Now, In ΔAOB,
∠O+∠A+∠B=180∘
160∘+x+x=180∘
2x=20∘
x=10∘
∴ Hence, option (a) is the correct answer.
|
Similar Questions
Knowledge Check
In the given figure , O is the centre of the circle . AP and AQ are tangents to the circle .∠PRQ=
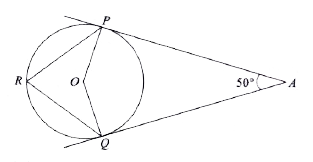 A55∘B45∘C75∘D65∘
A55∘B45∘C75∘D65∘In the figure, O is the centre of the circle . ∠PQR is equal to
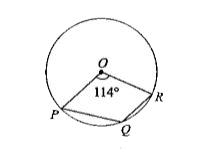 A57∘B63∘C123∘D92∘
A57∘B63∘C123∘D92∘In the given figure, O is the centre of the circle. Then ∠AED measure
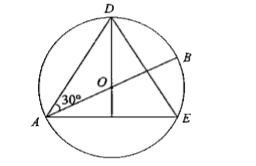 A30∘B45∘C60∘D90∘
A30∘B45∘C60∘D90∘
‘O’ is the centre of the circle. Find ∠(ADB)
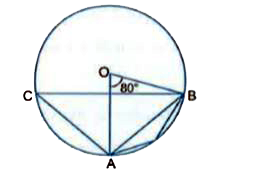
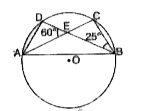
View SolutionIn the given figure, O is the centre of the circle. The measure of ∠ ADB is
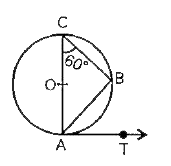
View SolutionIn the figure, O is the centre of a circle and AT is a tangent at point A. The measure of ∠BAT is:
View SolutionIf O is the centre of the circle then find ∠ADC
View SolutionIn the given figure (if O is the centre of circle.) , ∠COE measure
View Solution