H1 is a regular hexagon circumscribing a circle. H2 is a regular hexagon inscribed in the circle. Find the ratio of areas of H1andH2.
A
4:3
B
2:1
C
3:1
D
3:2
Video Solution
Text Solution
The correct Answer is:A
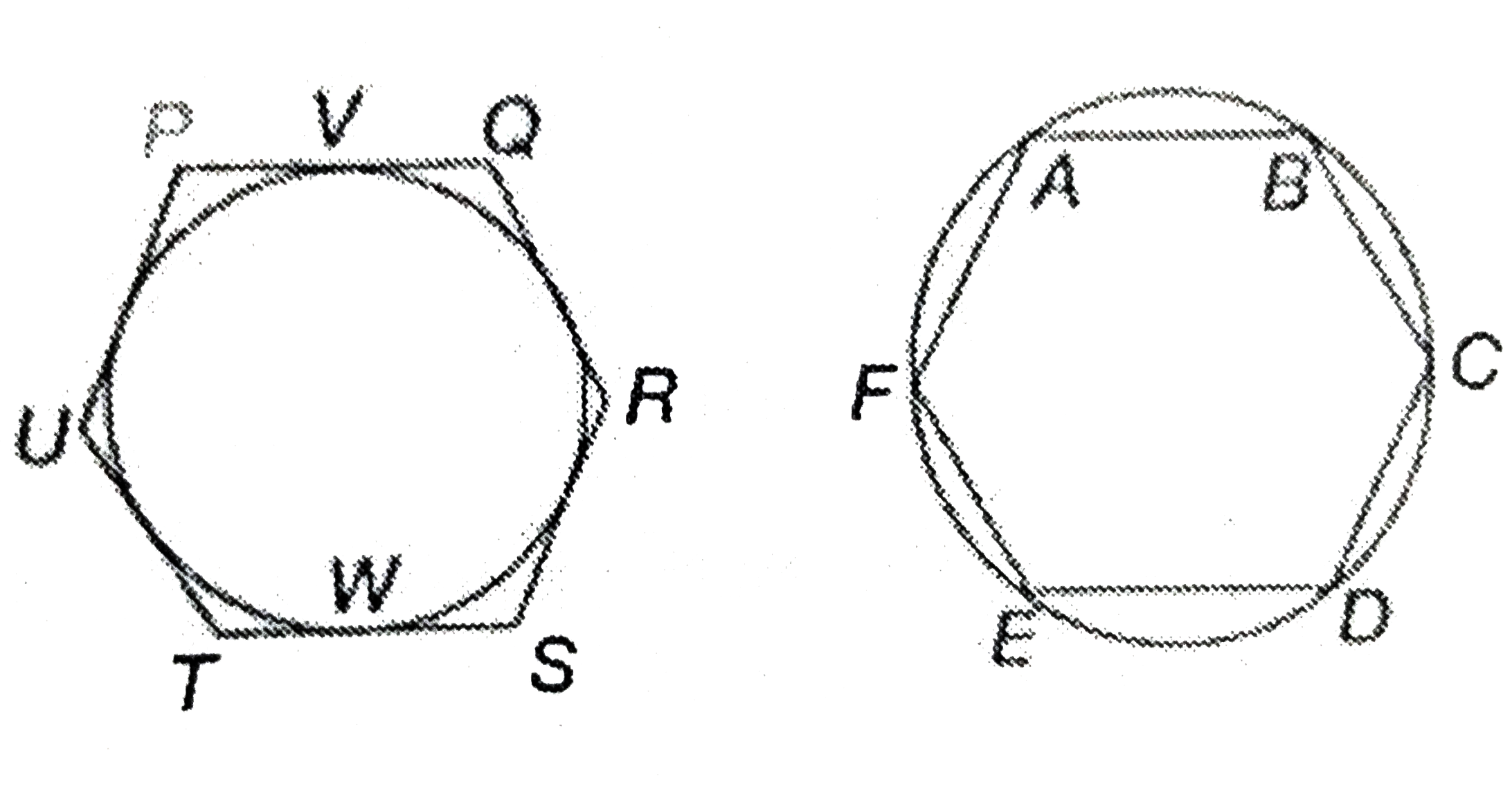
Let H1 be PQRSTU and H2 be ABCDEF.
Let R be the radius of the circle.
∴R=√3(PU)2⇒PU=2R√3
AB=R(∵A hexagon inscribed in a circle must have its side equal to the radius of the circle)
Area of H1=3√32(2√3R)2
And area of H2=3√32(R)2
(∵ Area of hexagon=3√32×(Its side)2)
Required ratio =(2√3R)2R2=43.
|
Similar Questions
Knowledge Check
What is the area of a regular hexagon inscribed in a circle of radius r ?
A2√3r2 sq. unitsB3√32r2 sq. unitsC23r2 sq. unitsD√32r2 sq. unitsIf a regular hexagon circumscribes a circle of radius r , then its perimeter is :
A4√3rB6√3rC6rD12√3rIf a regular hexagon circumscribes a circle of radius r , then its perimeter is :
A4√3rB6√3rC6rD12 sqrt3r
ABCDEF is a regular hexagon of side 6 cm. find the area of square BCEF
View SolutionIf the area of circle is A1 and area of regular pentagon inscibed in the circle is A2, then find the ratio of area of two.
View SolutionRatio of radius of circumscribing circle to that of incircle of regular hexagon is
View SolutionIf a regular hexagon circumscribes a circle of radius r , then its perimeter is :
View SolutionArea of a regular hexagon with side ‘a’ is
View Solution