Calculate the electric field due to a dipole on its axial line and equatorial plane. Solution in Tamil
Electric field due to an electric dipole at points on the axial line. Consider an electric dipole placed on the x-ax is as shown in figure. A point C is located at a distance of r from the midpoint O of the dipole along the axial line,.

→E=14πε0q(r−a)2 along BC
since the electric dipole moment vector →p is from -q to +q and is directed along BC, the above equation is rewritten as
→E+=14πɛ0q(r−a)2ˆp ........(1)
→E=14πɛ0q(r−a)2ˆp ...........(2)
where ˆp is located closer to the point C than −q,→E−.→E+ us stronger than →E− . therefore the length of the →E+ vector is drawn large than that of →E− vector.
The total electric field at point C is calculated using the superposition of the electric field
→Etot=→E++→E− .............(3)
=14πɛ0q(r−a)2ˆp−14πɛ0q(r−a)2ˆp⇒→Etot=14πɛ0(1(r−a)2−1(r+a)2)ˆp ............(4)
→Etot=14πɛ0q(4ra(r2−a2)2)ˆp ..............(5)
Note that total electric field is along →E+ since +q is closer to C than -q.
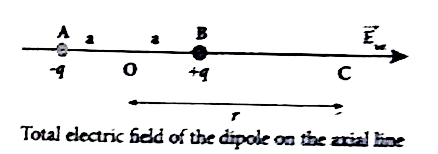
The direction of →Etot is shown in figure
If the point C is very far away from the dipole then (r>>a) .
Under this limit the term (r2−a2)2≈r4 Substituting this into equation we get
→Etot=14πɛ0(4aqr3)ˆp(r>>a)
since 2aq ˆp=→p
→Etot14πɛ02→pr3(r>>a)
If the C is chosen on the left side of the dipole the total electric field is still in the direction of →p .
Case (ii) Electric field due to an electric dipole at a point on the equatorial plane
Consider a point C at a distance r from the midpoint O of the dipole on the equatorial plane as shown in figure. since the point C is equi-distance from +q and -q , the magnitude of the electric field of +q and -q are the same. The direction of →E+ is along BC and the direction of →E− is along CA.
→E+and→E− are resolved into two components one component parallel to the dipole axis and the other perpendicular to it . The perpendicular components ∣∣→E−∣∣sinθand∣∣→E−∣∣sinθ are oppositely directed and cancel each other. The magnitude of the total electric field at point C is
the sum of the parallel components of →E+and→E− and its direction is along −ˆp.
→Etot=−∣∣→E+∣∣cosθˆp−∣∣→E−∣∣cosθˆp ........(1)
The magnitude →E+and→E− are the same and are given by
∣∣→E+∣∣=∣∣→E−∣∣=14πɛ0q(r2+a2) ..............(2)
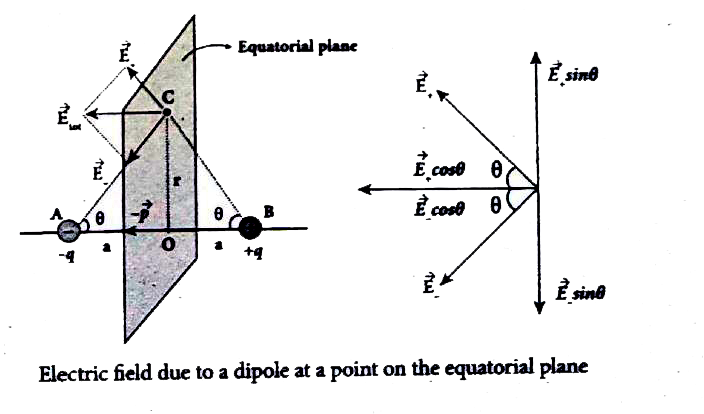
By substituting equation (1) into equation (2) ,we get
→Etot=−14πɛ02qcosθ(r2+a2)ˆp=−14πɛ02qa(r2+a2)32ˆp sinc cosθ=a√r2+a2
→Etot=−14πɛ0→p(r2+a2)32 since →p=2qaˆp ............(3)
At very large distance (r>>a) the equation becomes
→Etot=−14πɛ0pr3(r>>a) ............(4)
Similar Questions
If Ea be the electric field strength of a short dipole at a point on its axial line and Ee that on the equatorial line at the same distance, then
View SolutionIf Ea be the electric field strength of a short dipole at a point on its axial line and Ee that on the equatorial line at the same distance, then
View SolutionIf E1 is the electric field strength of a short dipole on its axial line and E2 that on the equatorial line at the same distance, then
View SolutionElectric Field Due to Dipole-Axial and Equatorial Position||Electric Potential Due to Dipole - Axial and Equatorial Position||E and V Due to a Dipole at a General Point
View SolutionElectric Dipole#!#Electric Field due to an electric dipole on its axial line
View Solutionकिसी विधुत द्विध्रुव के कारण इसकी अक्ष व विषुवतीय तल पर विधुत क्षेत्रो का अनुपात होगा
View SolutionElectric field due to dipole#!#Axial point#!#Equatorial Points
View SolutionThe electric field due to small dipole at a distance r from centre of dipole on axial is E. Find the distance on the equatorial line to have same electric field.
View Solution
