An artist has completed one-fourth of a rectangular oil painting. When he will paint another 100 square centimetres of the painting, he would complete three-quarters of the painting. If the height of the oil painting is 10 cm, determine the length (in cm) of the oil painting. (a) 10 (b) 15 (c) 20 (d) 25
To solve the problem, we need to determine the length of the rectangular oil painting given that the height is 10 cm and the area completed by the artist.
1. Define the Area of the Painting:
Let the total area of the painting be A square centimeters. The area of a rectangle is given by the formula:
A=length×height
2. Identify the Completed Areas:
The artist has completed one-fourth of the painting, which means:
Area completed=14A
After painting another 100 square centimeters, he will have completed three-quarters of the painting:
Area completed after additional painting=34A
3. Set Up the Equation:
The equation can be set up as follows:
14A+100=34A
4. Simplify the Equation:
Rearranging the equation gives:
100=34A−14A
100=24A
100=12A
5. Solve for the Total Area A:
Multiplying both sides by 2:
A=200 square centimeters
6. Calculate the Length of the Painting:
Given that the height of the painting is 10 cm, we can find the length L using the area formula:
A=L×height
Substituting the known values:
200=L×10
Solving for L:
L=20010=20 cm
Conclusion:
The length of the oil painting is 20 cm.
Let the total area of the painting be A square centimeters. The area of a rectangle is given by the formula:
A=length×height
The artist has completed one-fourth of the painting, which means:
Area completed=14A
After painting another 100 square centimeters, he will have completed three-quarters of the painting:
Area completed after additional painting=34A
The equation can be set up as follows:
14A+100=34A
Rearranging the equation gives:
100=34A−14A
100=24A
100=12A
Multiplying both sides by 2:
A=200 square centimeters
Given that the height of the painting is 10 cm, we can find the length L using the area formula:
A=L×height
Substituting the known values:
200=L×10
Solving for L:
L=20010=20 cm
The length of the oil painting is 20 cm.
Similar Questions
A rectangular parking space is marked out by painting three of its sides. If the length of the unpainted side is 9 feet, and the sum of the lengths of the painted sides is 37 feet, then what is the area of the parking space in square feet? (a) 46 (b) 81 (c) 126 (d) 252
View SolutionThe floor of a rectangular hall has a perimeter 250m . If the cost of painting the four walls at the rate of 10 per m2 is Rs.15000. Find the height of the hall.
View Solution
Knowledge Check
The length and breadth of a painting is 15 cm and 10 cm respectively. A 1 cm wide boarder is made around the painitng.
What is the area of boarder?A60 sq cm.B45 sq cm.C54 sq cm.D16 sq cm.The cost of painting the T.S.A. of a cone at 5 paise/ cm2 is Rs 35.20. If its slant height is 25 cm, then its volume is
A1223 cm3B1232 cm3C1323 cm3D1332 cm3
The area of a square sheet is 250 sq. cm. If one-fourth of the sheet is painted red, then half of the sheet is painted green and the remaining is painted white. Find the percentage of the area painted in white.
View SolutionA cubical box with lid has a length of 30cm .Find the cost of painting the inside and outside of the box at 25.50 per square metre
View SolutionAn aluminium - alloy rod has a length of 10.000 cm at 20.000∘C and a length of at the oiling point of water . (a) what is the length of the rod at the freezing point of water ? What is the temperature if the length of the rod is 10.009 cm?
View SolutionThe floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of Rs 10 per m2is Rs 15000, find the height of the hall.[Hint : Area of the four walls = Lateral surface area.]
View Solution10 cylindrical pillars of a building have to be painted. The diameter of each pillar is 70cm and the height is 4m. What is the cost of painting at the rate of Rs 5 per square metre
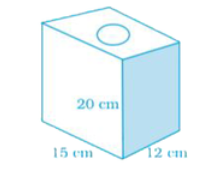
View SolutionFind the area to be painted in the following block with a cylindrical hole. Given that length is 15 cm, width 12 cm, height 20 cm and radius of the hole 2.8 cm.
View Solution