The vertices of a closed convex polygon representing the feasible region of the objective function are (6,2),(4,6),(5,4) and (3,6). Find the maximum value of the function f=7x+11y
61
69
59
49
The correct Answer is:B
Step by step video, text & image solution for The vertices of a closed convex polygon representing the feasible region of the objective function are (6,2),(4,6),(5,4) and (3,6). Find the maximum value of the function f=7x+11y by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The vertices of a closed convex polygon representing the feasible region of the objective function are (6,2),(4,6),(5,4) and (3,6). Find the maximum value of the function f=7x+11y
View Solutionlimn→∞1+4+9+16+...+n24n3+1=_______.
View SolutionThe solution set for |1−x|log10(x2−5x+5)=1, is ______.
View SolutionThe feasible region for an LPP is shown in the following figure. Let F=3x−4y be the objective function. Maximum value of F is
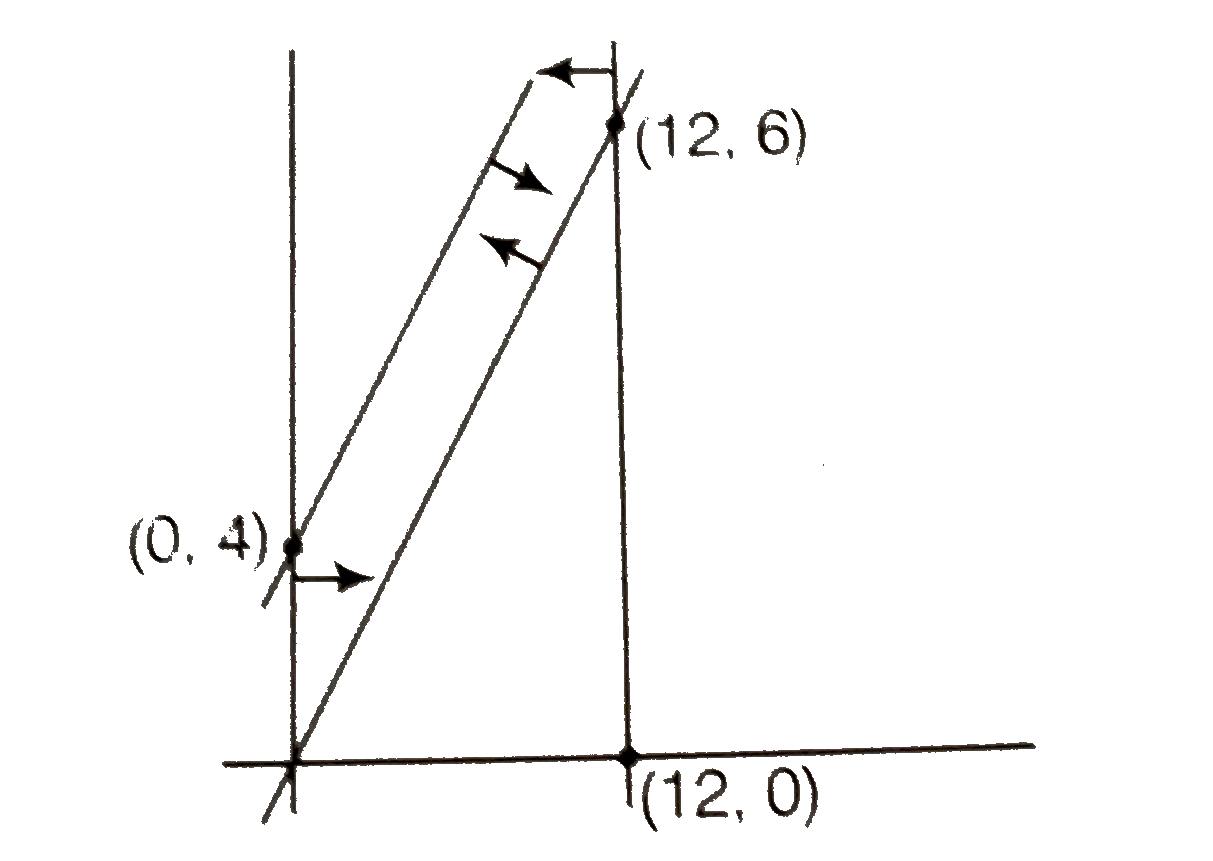
View SolutionThe vertices of a closed convex polygon representing the feasible region of the objective function are (6,2),(4,6),(5,4) and (3,6). Find the maximum value of the function f=7x+11y
View SolutionIf the vertices of a closed - convex polygon are A(8,0), O(0,0), B (20,10), C(24,5) and D(16,20), then find the maximum value of the objective function f=14x+15y.
View SolutionThe vertices of a closed - convex polygon representing the feasible region of the objective function f are (4,0), (2,4),(3,2) and (1,4) . Find the maximum value of the objective function f=7x+8y.
View SolutionThe vertices of a closed - convex polygon representing the feasible region of the objective function f =5x+3y , are (0,0),(3,0),(3,1),(1,3) and (0,4) . Find the maximum value of the objective function.
View SolutionThe maximum value of objective function z=2x+3y in the given feasible region is
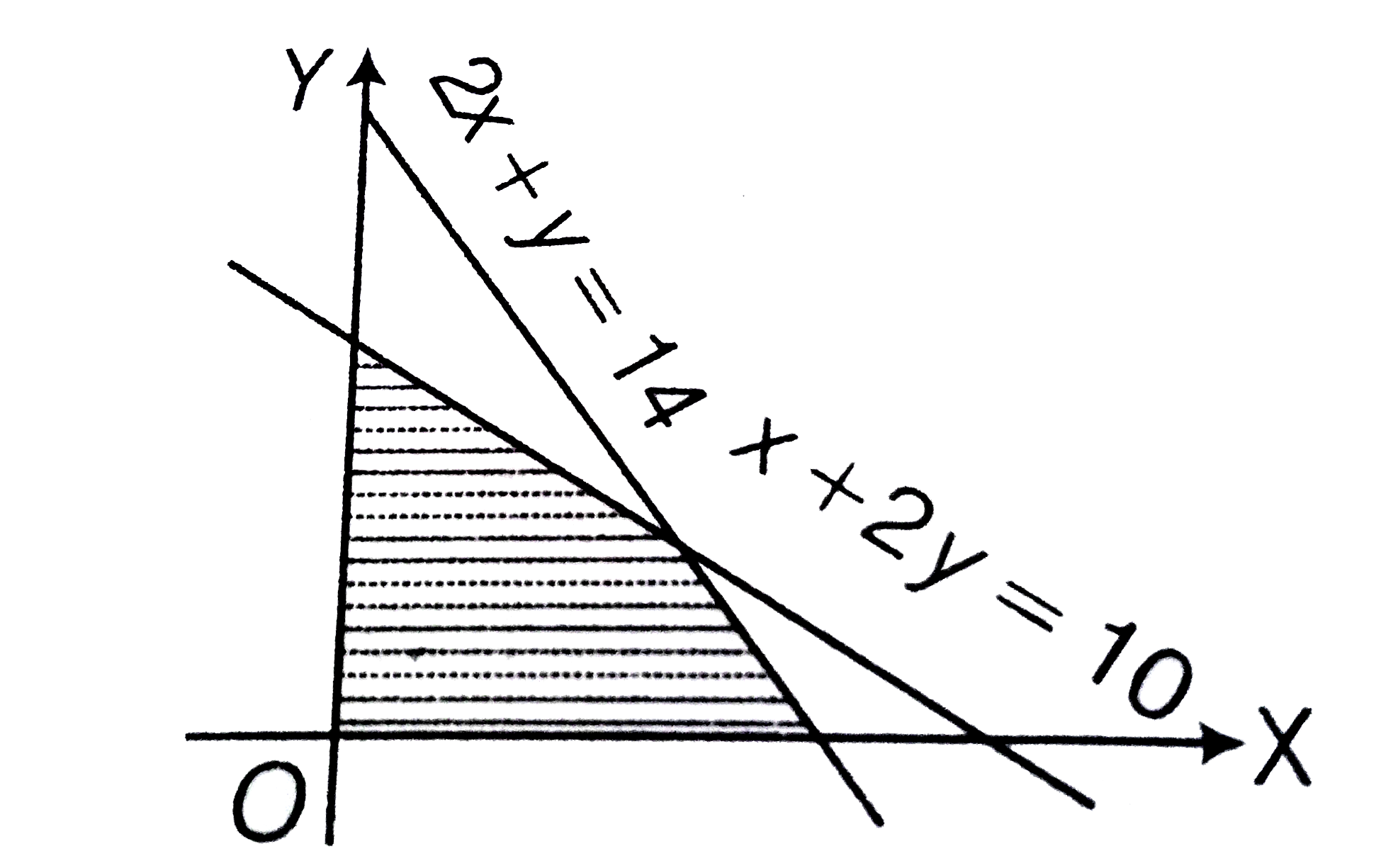
View SolutionConsider the following statements
I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
Which of the following statements are true?
View Solutionकिसी रैखिक प्रोग्रामन की समस्या में उद्देश्य फलन z=3x+8y का अधिकतमीकरण होना है और इसका सुसंगत क्षेत्र एक उत्तल बहुभुज से परिबद्ध है जिसके कोने (0,3), (5,4), (8,0) और (0,0) है | z का अधिकतम मान होगा
View SolutionThe vertices of a polygon in a feassible region are (2,-3), (3,3) and (-4,2), The maximimum value of the objective function F=2x+3y is
View SolutionThe, objective function is maximum or minimum at a point, which lies on the boundary of the feasible region.
View SolutionThe feasible region for an LPP is shown in the following figure. Let F=3x−−4y be the objective function. Maximum value of F is

View SolutionThe feasible region for an LPP is shown in the following figure. Let F=3 x-4 y be the objective function. Maximum value of F is

View Solution
