In a triangle PQR, PQ = 20 cm and PR = 6 cm, the side QR is :
equal to 14 cm
less than 14 cm
greater than 14 cm
none of these
The correct Answer is:C
To find the length of side QR in triangle PQR, we can use the triangle inequality theorem. The theorem states that for any triangle, the sum of the lengths of any two sides must be greater than the length of the third side, and the difference of the lengths of any two sides must be less than the length of the third side.
1. Identify the sides of the triangle:
- Given:
- PQ = 20 cm
- PR = 6 cm
- We need to find QR.
2. Apply the triangle inequality theorem:
- According to the theorem, we have the following inequalities:
1. PQ + PR > QR
2. PQ + QR > PR
3. PR + QR > PQ
3. Substituting the known values:
- From the first inequality:
- 20 cm + 6 cm > QR
- 26 cm > QR
- Thus, QR < 26 cm
- From the second inequality:
- 20 cm + QR > 6 cm
- QR > 6 cm - 20 cm
- QR > -14 cm (This inequality is always true since lengths cannot be negative)
- From the third inequality:
- 6 cm + QR > 20 cm
- QR > 20 cm - 6 cm
- QR > 14 cm
4. Combine the results:
- From the inequalities we derived:
- 14 cm < QR < 26 cm
5. Conclusion:
- The length of side QR must be greater than 14 cm and less than 26 cm. Therefore, QR can take any value in the range (14 cm, 26 cm).
- Given:
- PQ = 20 cm
- PR = 6 cm
- We need to find QR.
- According to the theorem, we have the following inequalities:
1. PQ + PR > QR
2. PQ + QR > PR
3. PR + QR > PQ
- From the first inequality:
- 20 cm + 6 cm > QR
- 26 cm > QR
- Thus, QR < 26 cm
- 20 cm + QR > 6 cm
- QR > 6 cm - 20 cm
- QR > -14 cm (This inequality is always true since lengths cannot be negative)
- 6 cm + QR > 20 cm
- QR > 20 cm - 6 cm
- QR > 14 cm
- From the inequalities we derived:
- 14 cm < QR < 26 cm
- The length of side QR must be greater than 14 cm and less than 26 cm. Therefore, QR can take any value in the range (14 cm, 26 cm).
Similar Questions
Knowledge Check
In △PQR,PQ=4,QR=6 and PR = 5. Then, ........ is the angle with greatest measure in △PQR.
A∠PB∠QC∠RD∠QPRIn ΔPQR, If ∠R=∠P, QR=4 cm and PR = 5 cm. Then, the length of PQ is
A4 cmB5 cmC2 cmD2.5 cmIn a triangle PQR,∠Q=90∘. If PQ=12cm and QR=5 cm, then what is the radius ( in cm ) of the circumcircle of the triangle ?
A5B6C6.5D6√2
In fig , a circle isinscribed in a triangle PQR with PQ = 10 cm , QR = 8 cm and PR = 12 cm .Find the length of the QM , RN and PL.
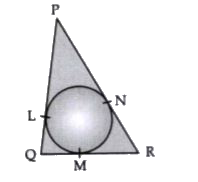
View SolutionIn △PQR,PQ=10 cm , QR =12 , PR =8 cm . Find out the greatest and the smallest angle of the triangle .
View SolutionIn △ XYZ, XY =4cm , YZ =6 cm , XZ =5 cm. If △ XYZ △PQR and PQ =8 cm then find QR and PR.
View SolutionTriangle PQR is a right-angled at Q. If PQ=6 cm , PR=10 cm, then QR is equal to:
त्रिभुज PQR एक समकोण त्रिभुज है जिसमें Q समकोण है | यदि PQ = 6 सेमी, PR = 10 सेमी है, तो QR किसके बराबर होगा ?
View SolutionA circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR = 12 cm. Find the lengths QM, RN and PL.
View Solution
