If P is a point within a rectangle ABCD, then:
AP2+PC2=BP2+PD2
AP2+BP2=PC2+PD2
AP+PC=BP+PD
AP×PC=BP×PD
The correct Answer is:A
To solve the problem, we need to analyze the situation where P is a point inside rectangle ABCD. We will derive the relationship involving the distances from point P to the vertices of the rectangle.
1. Draw the Rectangle and Point P:
- Start by drawing rectangle ABCD with vertices A, B, C, and D in clockwise order.
- Place point P inside the rectangle.
2. Label the Distances:
- Let the distances from point P to the vertices be:
- PA = distance from P to A
- PB = distance from P to B
- PC = distance from P to C
- PD = distance from P to D
3. Identify the Right Triangles:
- From point P, draw lines to each vertex of the rectangle. This creates four triangles: PAB, PBC, PCD, and PDA.
- Each of these triangles contains a right angle at the vertices of the rectangle.
4. Apply Pythagorean Theorem:
- For triangle PAB:
PA2=PX2+PY2(1)
- For triangle PBC:
PB2=PY2+PC2(2)
- For triangle PCD:
PC2=PY2+PD2(3)
- For triangle PDA:
PD2=PX2+PA2(4)
5. Combine the Equations:
- Now, we can add equations (1) and (3):
PA2+PC2=PX2+PY2+PY2+PD2
- Similarly, add equations (2) and (4):
PB2+PD2=PY2+PC2+PX2+PA2
6. Rearranging:
- Rearranging gives us:
PA2+PD2=PB2+PC2
7. Final Result:
- Thus, we conclude that:
PA2+PD2=PB2+PC2
Conclusion:
The relationship derived shows that the sum of the squares of the distances from point P to two opposite corners of the rectangle is equal to the sum of the squares of the distances to the other two corners.
- Start by drawing rectangle ABCD with vertices A, B, C, and D in clockwise order.
- Place point P inside the rectangle.
- Let the distances from point P to the vertices be:
- PA = distance from P to A
- PB = distance from P to B
- PC = distance from P to C
- PD = distance from P to D
- From point P, draw lines to each vertex of the rectangle. This creates four triangles: PAB, PBC, PCD, and PDA.
- Each of these triangles contains a right angle at the vertices of the rectangle.
- For triangle PAB:
PA2=PX2+PY2(1)
- For triangle PBC:
PB2=PY2+PC2(2)
- For triangle PCD:
PC2=PY2+PD2(3)
- For triangle PDA:
PD2=PX2+PA2(4)
- Now, we can add equations (1) and (3):
PA2+PC2=PX2+PY2+PY2+PD2
- Similarly, add equations (2) and (4):
PB2+PD2=PY2+PC2+PX2+PA2
- Rearranging gives us:
PA2+PD2=PB2+PC2
- Thus, we conclude that:
PA2+PD2=PB2+PC2
The relationship derived shows that the sum of the squares of the distances from point P to two opposite corners of the rectangle is equal to the sum of the squares of the distances to the other two corners.
Topper's Solved these Questions
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.4
Explore 10 Videos
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.5
Explore 60 Videos
- GEOMETRYBook:ARIHANT SSCChapter:GEOMETRYExercise:INTRODUCTORY EXERCISE - 12.2
Explore 100 Videos
- FUNDAMENTALS Book:ARIHANT SSCChapter:FUNDAMENTALS Exercise:TEST OF YOU - LEARNING - 2
Explore 40 Videos
- HCF AND LCMBook:ARIHANT SSCChapter:HCF AND LCMExercise:Exercise Higher Skill Level Questions
Explore 18 Videos
Similar Questions
Each interior angle of a regular polygon is 140∘. The number sides is :
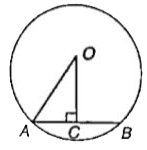
View SolutionIn the given figure, O is the centre of the circle. Radius of the circle is 17 cm. lf OC=8cm, then the length of the chord AB is :
View SolutionIn a triangle ABC, if AB,BC and AC are the three sides of the triangle, then which of the statements is necessarily?
View SolutionThe remainder when 888222888222888222… upto 9235 digits is divided by 53 is :
View SolutionIf (x-6) is the HCF of x2−2x−24 and x2−kx−6, then what is the value of k is
View SolutionOne of the diameters of circle circumscribing the rectangle ABCD is4y=x+7. If A and B are the points (−3,4) and (5,4) respectively and area of rectangle is p then p4 is equal to
View Solutionयदि ABCD एक आयत है और P आयत में एक बिन्दु है , तब सिध्द करे की PA2+PC2=PB2+PD2
View Solution
In rectangle ABCD, point P divide BC such that BP is 25% of the length of BC. If the area of quadrlateral ABPD is 34, what is the area of rectangle ABCD?
View SolutionDiagonal of a rectangle ABCD intersect at point P,∠BPC=50∘. Then find ∠PAD.
View SolutionIn the given figure, if ABCD is a rectangle and P, Q are the mid-points of AD, DC respectively. then, the ratio of lengths PQ and AC is equal to
View SolutionABCD is a rectangle and P,R and S are the mid - points of the AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View Solutionआयत ABCD के अंदर स्थित O कोई बिंदु है सिद्ध कीजिये

View SolutionIn a rectangle ABCD, P,Q are the mid-points of BC and AD respectively and R is any point on PQ, then ΔARB equals :
View SolutionThe points A(1,2),B(3,-4) are two vertices of the rectangle ABCD. The point P(3,8) lies on the CD produced then C=
View SolutionABCD एक समचतुर्भुज है। AB,BC,CD,DA के मध्य-बिंदु क्रमशः P,Q,R,S हैं। सिद्ध कीजिए कि PQRS एक आयत है।
View Solution