A bead of mass m is fitted on a rod and can move on it without friction. Initially the bead is at the middle of the rod moves transitionally in the vertical plane with an accleration a0 in direction forming angle α with the rod as shown. The acceleration of bead with respect to rod is:
z
Let ar be the acceleration of the bead relative to the rod. Then arcosα is the leftward horizontal acceleration of the bead relative to the rod and arsinα is downward relative acceleration of the rod. If axanday be the absolute leftward horizontal and downward vertical acceleration of the bead
arcosα−ax−a
(∵ relative acceleration is simply the vector difference between the absolute acceleration)
or, ax=arcosα+a ...(1)
and arsinα=ay−0
or, ay=arsinα ...(2)
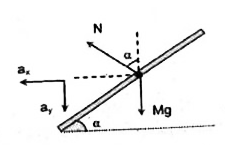
From FBD of the bead (projecting forces vertically and horizontally)
mg−Ncosα=marsinα ...(3)
and Nsinα=m(arcosα+a) ...(4)
Eliminating N between (3) and (4)
mgsinα=mar+macosα
or ar=gsinα−acosα
Similar Questions
An underformed spring of spring constant k is connected to a bead of mass m as shown in figure. Bead can move along long rigid rod without friction. A particle of mass moving with velocity v in the vertical plane containing spring and rod strikes bead at an angle 45^(@) with horizontal and sticks to bead. Choose correct alternative representing maximum elongation of spring is, all particles are in same horizontal plane.
View SolutionA smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity ω0 about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......

View SolutionTwo similar beads each of mass m slide smoothly along a uniform rod mass M and length l. the rod can rotate along an axis passing through its centre and normal to its length. Initially the rod is rotated with angular speed ωi when beads are at centre C of the rod. The engular speed ωf of the rod when beads slide to the two ends of the rod without any external force is given by Mωi(xm+M) where 'x' is

View SolutionA small bead of mass M is launched from the end of a horizontal rod at a speed u along rod having same mass M. The rod is free to rotate in a vertical plane about a end. Simultaneously the rod is given a angular velocity omega as shown in the figure. Find the angular acceleration of the rod. [The rod is hinged at an end]
View Solutionएक लम्बी क्षैतिज छड़ पर एक मोती पिरोया गया है, यह छड़ कि लम्बाई के अनुदिश फिसल सकता है और प्रारम्भ में यह छड़ के एक सिरे A से L दुरी पर है । छड़ को A के पारित नियत कोणीय त्वरण α से घुमाया जाता है । यदि छड़ एवं मोती के बीच घर्षण गुणांक μ है और गुरुत्व को नगण्य माना जाये तो कितने समय पश्चात मोती फिसलना प्रारम्भ कर देगा ?
View SolutionA bead of mass m is fitted on a rod and can move on it without friction. Initially the bead is at the middle of the rod moves transitionally in the vertical plane with an accleration a_(0) in direction forming angle alpha with the rod as shown. The acceleration of bead with respect to rod is: z
View SolutionA thin rod of length 1m is fixed in a vertical position inside a train, which is moving horizontally with constant acceleration 4ms−2.A bead can slide on the rod and friction coefficient between them is 0.5. If the bead is released from rest at the top of the rod , it will reach the bottom in
View SolutionA rod can rotate in a horizontal plane about its one end. A bead which can move along the rod is placed at certain distance from the axis or rotation. The bead does not to friction. The rod has a constant angular acceleration A. the normal reaction on the bead will be constant h magnitude and direction both B. the magnitude of the normal reaction on the bead will be variable C. the magnitude of friction force on the bead will be constant D. the magnitude of friction force on the bead will be variable
View Solution

