Masses M1,M2andM3 are connected by string of negligible mass which pass over massless and frictionless pulleys P1andP2 as shown in figure 7.15. The masses move such that the string between P1andP2 is parallel to the incline and the portion of the string between P2andM3 is horizontal. The masses M2andM3 are 4.0 kg each and the coefficient of kinetic friction between the masses and the surfces is 0.25. The inclined plane makes an angle of 37∘ with the horizontal. If the mass M1moves downwards with a uniform velocity, find (i) the mass of M1, (ii) the tension in the horizontal portion. (g=9.8ms−2,sin37∘=35)
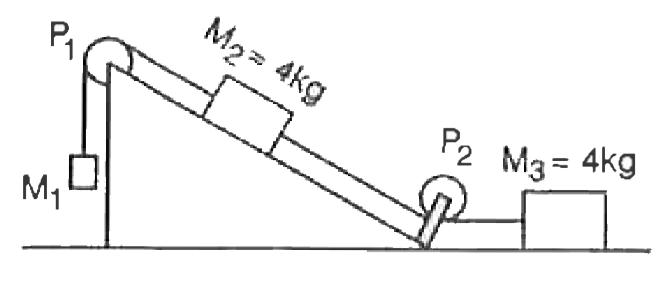
Let T1 be the tension in the string connecting M1andM2andT2 be the tension in the string connecting M2andM3. From the figure.
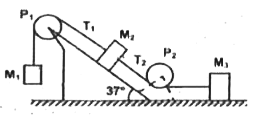
M1g=T1
T2=μM3g=(0.25)4g
Or, T2=g=9.8N
Also
T1=T2+(0.25)×4gcos37∘+4gsin37∘
=g(1+45+4×35)
T1=215g
Or, M1g=215g
∴M1=215=4.2kg
Similar Questions
तीन द्रव्यमान M1,M2 तथा M3 एक नगण्य द्रव्यमान वाली डोरी द्वारा जुड़े जो कि नगण्य द्रव्यमान वाले घर्षण रहित घिरनियाँ P1 व P2 से चित्रानुसार गुजरती है। द्रव्यमान इस प्रकार गति कहते है कि P1 व P2 के बीच डोरी का भाग नत समतल के समान्तर रहता है तथा P2 व P3 के बीच का भाग क्षैतिज रहता है । M2 तथा M3 में से प्रत्येक का द्रव्यमान 4.0 किग्रा तथा द्रव्यमानों व तालों के बीच का गतिज घर्षण गुणांक 0.25 है। नत समतल क्षैतिज से 37∘ का कोण बनता है। यदि M1 नीचे की और समान वेग से गतिमान हो तो ज्ञात कीजिए :
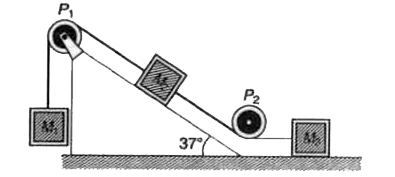 .
.
(g=9.8मी/से2,sin37∘=3/5).
(a) द्रव्यमान M1
(b) डोरी के क्षैतिज भाग में तनाव
View SolutionMasses M1,M2andM3 are connected by string of negligible mass which pass over massless and frictionless pulleys P1andP2 as shown in figure 7.15. The masses move such that the string between P1andP2 is parallel to the incline and the portion of the string between P2andM3 is horizontal. The masses M2andM3 are 4.0 kg each and the coefficient of kinetic friction between the masses and the surfces is 0.25. The inclined plane makes an angle of 37∘ with the horizontal. If the mass M1moves downwards with a uniform velocity, find (i) the mass of M1, (ii) the tension in the horizontal portion. (g=9.8ms−2,sin37∘=35)

View SolutionTwo masses m1kg and m2kg passes over a pulley. Find the ratio of the masses m1andm2 so that string passes over the pulley will just start slipping over is surface. The friction coefficient between the string and pulley surface is 0.2
View SolutionTwo masses m1kg and m2kg passes over a pulley. Find the ratio of the masses m1andm2 so that string passes over the pulley will just start slipping over is surface. The friction coefficient between the string and pulley surface is 0.2
View SolutionA massless string passes over a frictionless pulley and carries mass m_(1) hanging at one end and mass m_(2) connected by another massless string to mass m_(3) at other end as shown in figure . Calculate the tension in string joining masses m_(2)"and " m_(3) .
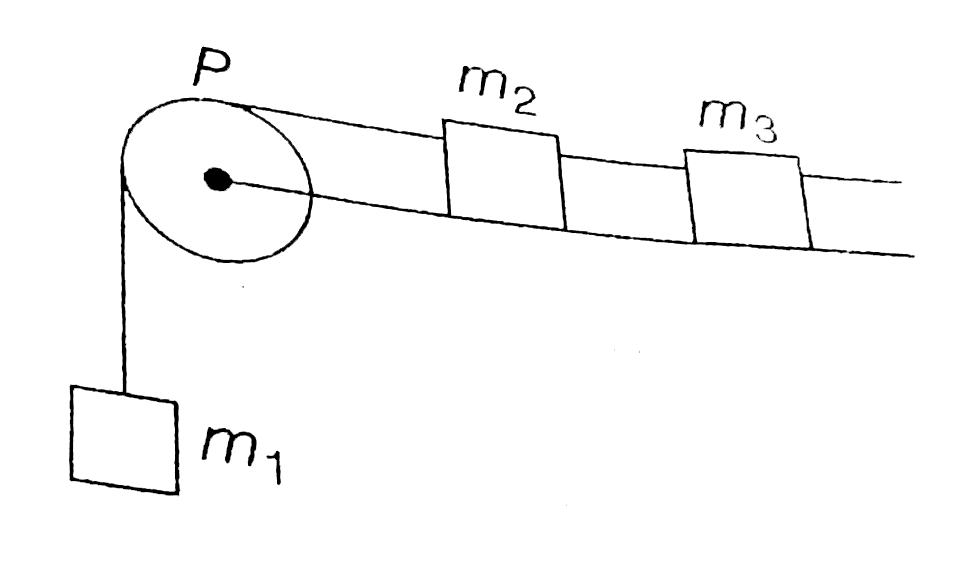
View SolutionA system consists of three masses m1,m2 and m3 connected by a string passing over a pulley P. The mass m1 hangs freely and m2 and m3 are on a rough horizontal table (the coefficient of friction=μ). The pulley is frictionless and of negligible mass. The downward acceleration of mass m1 is (assume, m1=m2=m3=m)
View SolutionThe block each of mass 1kg are placed as shown .They are connected by a string which passes over a smooth (massless) pulley.

There is no friction between m1 and the ground.The coefficient of friction between m1 andm2 is 0.2A force F is applied to m2. Which of the fpllowing statement is/are correct?
View SolutionA system consists of three masses m1 , m1 , m1 , m2 and m3 connected by a string passing over a pulley P . The mass m1 hangs freely and m2 and m3 are on a rough horizontal table (the coefficient of friction=mu) The pulley is frictionless and of negligible mass. The downward acceleration of m1 is (Assume m1=m2=m3=m).

View Solution
