A light string passing over a smooth light pulley connects two blocks of masses m_(1) and m_(2) (vertically).If the acceleration of the system is g/8 then the ratio of masses "m_(1)" to "m_(2)" is "(" take "m_(1)>m_(2)]
8:1
9:7
4:3
5:3
The correct Answer is:B
Step by step video, text & image solution for A light string passing over a smooth light pulley connects two blocks of masses m_(1) and m_(2) (vertically).If the acceleration of the system is g/8 then the ratio of masses "m_(1)" to "m_(2)" is "(" take "m_(1)>m_(2)] by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A light string passing over a smooth light pulley connects two blocks of masses m_(1) and m_(2) (vertically). If the acceleration of the system is g//8, then the ratio of the masses is:
View SolutionConsider the case of two bodies of masses m_(1) and m_(2) which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations: (i) when m_(1) gt m_(2) . In this case a=((m_(1)-m_(2))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (ii) when m_(2) gt m_(1) . In this case a=((m_(2)-m_(1))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (iii) When m_(1)=m_(2)=m . In this case a = 0, T = mg If m_(1)=10kg, m_(2)=6kg and g =10m//s^(2) then what is the acceleration of masses?
View SolutionConsider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
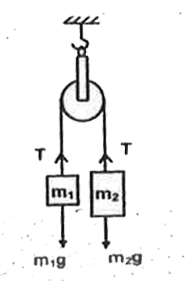
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
What is the tension in the string?
View SolutionConsider the case of two bodies of masses m_(1) and m_(2) which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations: (i) when m_(1) gt m_(2) . In this case a=((m_(1)-m_(2))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (ii) when m_(2) gt m_(1) . In this case a=((m_(2)-m_(1))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (iii) When m_(1)=m_(2)=m . In this case a = 0, T = mg If the pulley is pulled upward with acceleration equal to the acceleration due to gravity, what will be the tension in the string?
View SolutionTwo masses m1 and m2(m2>m1) are hanging vertically over frictionless pulley. The acceleration of the two masses is :

View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionThree blocks of masses m1,m2 and M are arranged as shown in figure. All the surfaces are fricationless and string is inextensible. Pulleys are light. A constant force F is applied on block of mass m1. Pulleys and string are light. Part of the string connecting both pulleys is vertical and part of the strings connecting pulleys with masses m1 and m2 are horizontal.
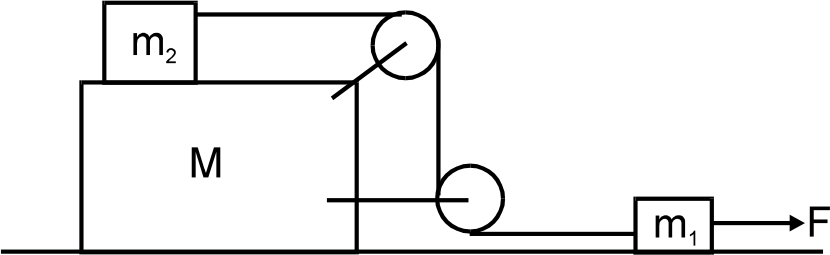
(P)Accleration of mass m1(1)Fm1(Q)Acceleration of massm2(2)Fm1+m2(R)Acceleration of mass M(3)zero(S)Tension in the string(4)m2Fm1+m2
View SolutionTwo masses m1 and m2(m2>m1) are hanging vertically over frictionless pulley. The acceleration of the two masses is :

View Solution

