A mass m is suspended from a spring of force constant k and just touches another idential spring fixed to the floras shown in the figure. The time period of small oscillation is

2π√mk
π√mk+π√mk/2
π√m3k/2
π√mk+π√m2k
The correct Answer is:D
When .m. moves slightly downward, then both spring are effecting for half period
t1=π√m2k
when mass moves upwards only
Upper spring is effective
t2=π√mk
∴ Time period T=t1+t2
T=π√m2k+π√mk
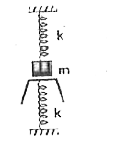
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Subjective) (Level)
Explore 20 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Subjective) (Level-II & III)
Explore 13 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Matrix Match Type
Explore 11 Videos
- SEMICONDUCTOR AND DEVICEBook:FIITJEEChapter:SEMICONDUCTOR AND DEVICEExercise:SOLVED PROBLEMS Objective: Level-I
Explore 20 Videos
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
Similar Questions
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

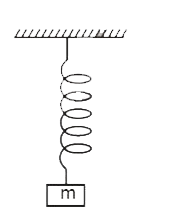
View SolutionA mass m is attached to the free end of a massless spring of spring constant k with its other end fixed to a rigid support as shown in figure. Find out the time period of the mass, if it is displaced slightly by an amount x downward.
View Solution
Knowledge Check

A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in the fig. The time period of small oscillations isA2π√mkBπ√mk+π√mk2Cπ√m3k2Dπ√mk+π√m2kA block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.
 A2π√mkB2π√m2kC2π√2mkDπ√m2k
A2π√mkB2π√m2kC2π√2mkDπ√m2kA block of mass m is suspended by different springs of force constant shown in figure.
 AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4
AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4
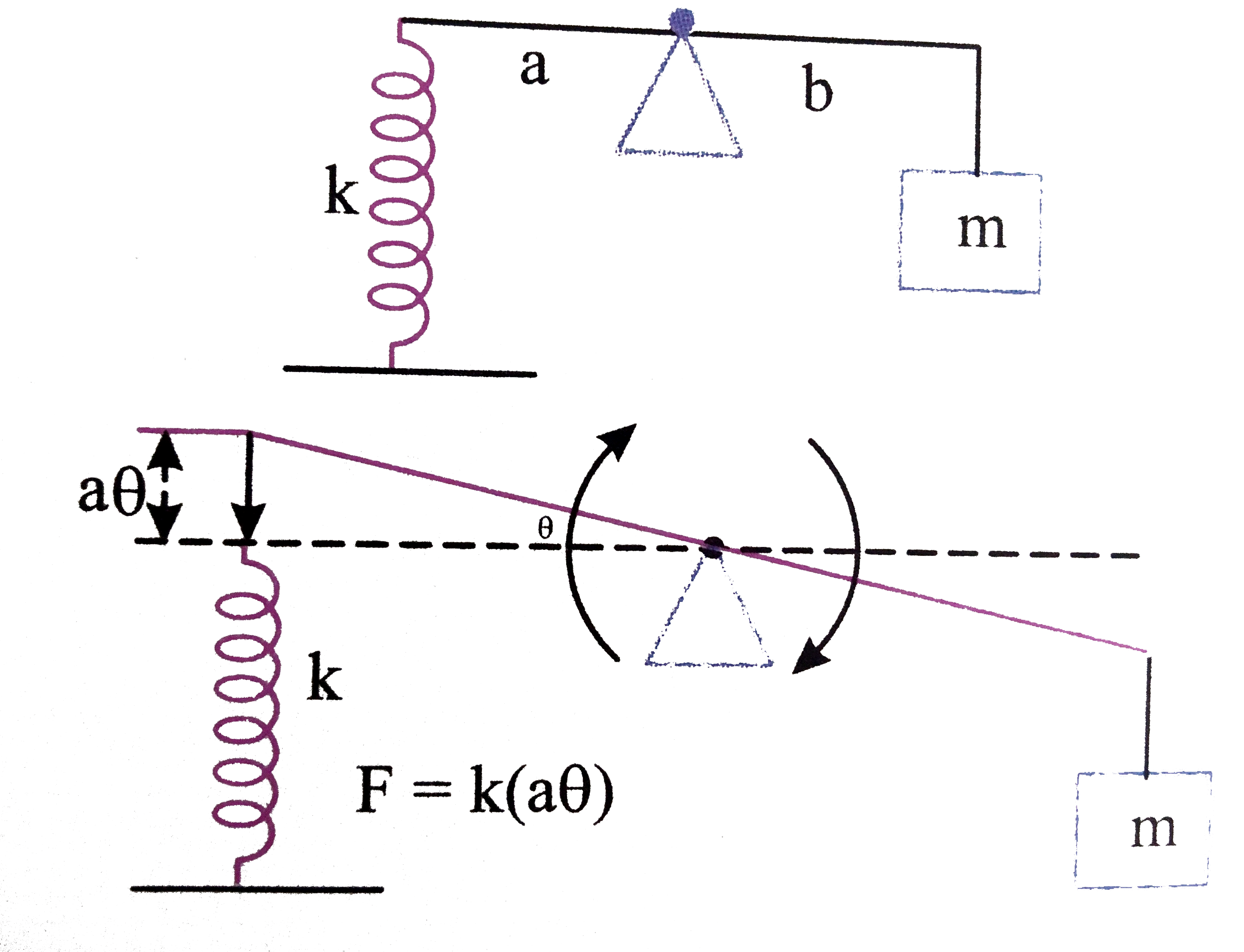
A small block is connected to a mass less rod, which is turn is attached to a spring of force constant k as shown in Fig. The blcok is displaced down slightly, and left free. Find time period of small oscillations.
View SolutionOne mass m is suspended from a spring. Time period of oscilation is T. now if spring is divided into n pieces & these are joined in parallel order then time period of oscillation if same mass is suspended.
View SolutionA particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is

View SolutionA uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:

View SolutionA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

View Solution

