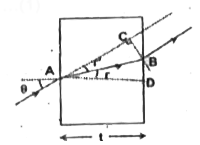
A ray of light strikes a glass slab of thickness t.
(i) Prove that it emerges on the opposite face, parallel to the initial ray.
(ii) (ii) Prove that the value of deflection of beam which passed through the plate is :
tsini1⎡⎢⎣1−
⎷(1−sin2i1.aμ2g−sin1i1)⎤⎥⎦
(iii) Prove that for a small angle of incidence i1, the internal shift x is given by
x=ti1(1−1.aμg)
where .aμg is the refractive index of glass with respect to air.
Video Solution
Text Solution
Lateral shift, y=BC=ABsinr.=ABsin(θ−r)
⇒y=tcosr(sinθ−cosθsinr)=t(sinθ−cosθtanr)
tsinθ(1−cotθtanr)…(2)
where AB= t/cosr and r= angle of refraction given by using snell.s law,
sinθsinr=n
⇒sinr=sinθn & cosr in (1) we obtain
y=tsinθ⎡⎢⎣1−cotθsinθn√n2−sin2θn⎤⎥⎦
=tsinθ[1−√1−sin2θn2−sin2θ]
(b) If θ is small, sin2θ can be ignored in comparison to 1, n2
⇒y≅tθ[1−√1n2]
⇒y=tθ[1−1n]
|
Similar Questions
If I1=∫π20(sinx)√3+1dx,I2=∫π20(sinx)√3−1)dx then I1I2=
View SolutionThe r.m.s. value of I = I_(1) sin omega t + I_(2) cos omega t is
View SolutionThe r.m.s. value of I = I_(1) sin omega t + I_(2) cos omega t is
View SolutionA ray of light is incident on a prism of refractive index μ and angle A at the angle of incidence i1 and emerges at the angle i2. If the ray is incident on the prism at the angle i2, calculate the deviation of the ray.
View SolutionIf I1=∫tanx1/et1+t2dtandI2=∫cotx1/edtt(1+t2) then the values of I1+I2 is
View SolutionIf I1∫sin−1(2x1+x2) dx ,
I2=∫cos−1(1−x21+x2) dx ,
I3=∫tan−1(2x1−x2) dx , then I1+I2−I3 =
View SolutionFor xεR, and a continuous function f let I1=∫1+cos2tsin2txf{x(2−x)}dx and I2=∫1+cos2tsin2tf{x(2−x)}dx.
Then I1I2 is
View SolutionIf In=∫sinnxcosxdx, prove that In=−2n−1cos(n−1)x−In−2
View Solution
